题目内容

如图是一个几何体的三视图，其中正视图与左视图都是全等的腰为
3
的等腰三角形，俯视图是边长为2的正方形，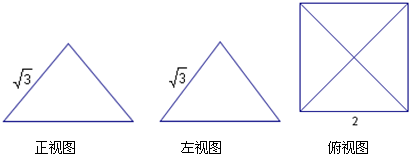
（1）画出该几何体；
（2）求此几何体的表面积与体积．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可知，该几何体为四棱锥，根据条件确定棱锥的高和边长，利用棱锥的体积公式和表面积公式计算即可．
解答： 解：（1）该几何体的直观图如图所示
（2）作斜高EF⊥BC，连接EO，OF，由正视图可知：EF=
3
，
在Rt△EOF中：EO=
EF2-OF2
=
3-1
=
2
，
∴S表面积=4S△EBC+SABCD=4×
1
2
×2×
3
+2×2=4
3
+4，
V=
1
3
×SABCD×EO=
1
3
×2×2×
2
=
4
2
3
．
点评：本题主要考查三视图的应用，利用三视图还原成空间几何体的直观图，是解决三视图问题的关键，要求熟练掌握锥体的体积公式和表面积公式．
练习册系列答案
相关题目
某学校有高一学生720人，现从高一、高二、高三这三个年级学生中采用分层抽样的方法，抽取180人进行英语水平测试．已知抽取的高一学生数是抽取的高二学生数、高三学生数的等差中项，且高二年级抽取40人，则该校高三学生人数是
 
．
已知甲、乙两种不同品牌的PVC管材都可截成A、B、C三种规格的成品配件，且每种PVC管同时截得三种规格的成品个数如下表：
A规格成品（个） B规格成品（个） C规格成品（个）
品牌甲（根） 2 1 1
品牌乙（根） 1 1 2
现在至少需要A、B、C三种规格的成品配件分别是6个、5个、6个，若甲、乙两种PVC管材的价格分别是20元/根、15元/根，则完成以上数量的配件所需的最低成本是（　　）
A、70元B、75元
C、80元D、95元
已知f（x）=（x-a）（x-b）-2，（a＜b），并且α，β是方程f（x）=0的两根，（α＜β），则实数a，b，α，β大小关系为
 
．
设f（x）为二次函数，f（0）=3，f（x+1）-f（x）=4x+2
（1）求f（x）的解析式；
（2）求f（x）在区间[-2，1]上的最大值和最小值．
已知{an}为等差数列，若a1+a5+a9=8π，则cos（a2+a8）的值为
 
．
已知f（x）是R上的奇函数，对x∈R都有f（x+4）=f（x）+f（2）成立，若f（1）=2，则f（2014）等于（　　）
A、2014B、2C、0D、-2
偶函数f（x）满足f（x-1）=f（x+1），且在x∈[0，1]时，f（x）=1-x，则关于x的方程f（x）=log9（x+1）解的个数是
 
个．
已知f（x）在（-1，1）上有定义，f(
1
2
)=1，且满足x，y∈（-1，1）时有f(x)-f(y)=f(
x-y
1-xy
)，数列{xn}满足x1=
1
2
，xn+1=
2xn
1+xn2
．
（1）求f（0）的值，并证明f（x）在（-1，1）上为奇函数；
（2）探索f（xn+1）与f（xn）的关系式，并求f（xn）的表达式；
（3）是否存在自然数m，使得对于任意的n∈N*，
1
f(x1)
+
1
f(x2)
+…+
1
f(xn)
＞
m-8
4
恒成立？若存在，求出m的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网