题目内容
已知f(x)=(x-a)(x-b)-2,(a<b),并且α,β是方程f(x)=0的两根,(α<β),则实数a,b,α,β大小关系为 .
考点:一元二次方程的根的分布与系数的关系
专题:综合题,探究型,数形结合
分析:方法一:首先把方程化为一般形式,由于α,β是方程的解,根据根与系数的关系即可得到a,b,α,β之间的关系,然后对四者之间的大小关系进行讨论即可判断.
方法二:可作出w=(x-a)(x-b)与y=(x-a)(x-b)-2的图象,由图象比较即可得到结论
方法二:可作出w=(x-a)(x-b)与y=(x-a)(x-b)-2的图象,由图象比较即可得到结论
解答:
解:方法1:方程化为一般形式得:x2-(a+b)x+ab-2=0,
∵α,β是方程(x-a)(x-b)-2=0的两根,∴α+β=a+b
f(α)=0,f(β)=0,f(a)<0,f(α)<0
又二次函数图象开口向上,∴必有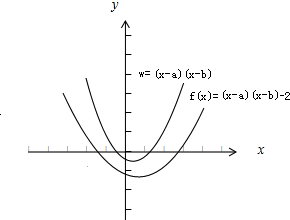 α<a<b<β;
α<a<b<β;
故答案为:α<a<b<β.
方法2:令w=(x-a)(x-b),作出图象抛物线与x轴交于点a,b.则y=(x-a)(x-b)-2的图象是将w向下平移2个单位得到,如图则α、β是抛物线y与x轴的两个交点.在图上可以直接看到α<a<b<β.
故答案为:α<a<b<β.
∵α,β是方程(x-a)(x-b)-2=0的两根,∴α+β=a+b
f(α)=0,f(β)=0,f(a)<0,f(α)<0
又二次函数图象开口向上,∴必有
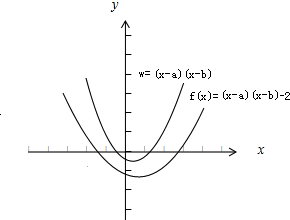 α<a<b<β;
α<a<b<β;故答案为:α<a<b<β.
方法2:令w=(x-a)(x-b),作出图象抛物线与x轴交于点a,b.则y=(x-a)(x-b)-2的图象是将w向下平移2个单位得到,如图则α、β是抛物线y与x轴的两个交点.在图上可以直接看到α<a<b<β.
故答案为:α<a<b<β.
点评:本题考查了一元二次方程的根与系数之间的关系,对a,b,α,β大小关系的讨论是此题的难点,是中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设x+x-1=3,则x3+x-3的值为( )
| A、18 | B、±6 | C、12 | D、6 |
在棱长为2的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )
A、
| ||
| B、8 | ||
C、
| ||
D、
|
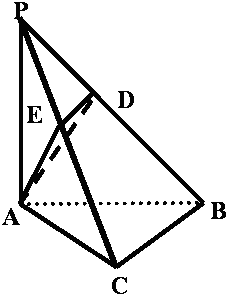 如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC
如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC
 某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).