题目内容
函数f（x）是定义域为{x|x≠0}的奇函数，且f（1）=1，f′（x）为f（x）的导函数，当x＞0时，f（x）+xf′（x）＞
，则不等式xf（x）＞1+ln|x|的解集为（ ）
| 1 |
| x |
| A、（-∞，-1）∪（1，+∞） |
| B、（-∞，-1） |
| C、（1，+∞） |
| D、（-1，1） |
考点：利用导数研究函数的单调性,奇偶性与单调性的综合
专题：导数的综合应用
分析：通过g（x））=xf（x）-ln|x|，为偶函数，且当x＞0时，g′（x）＞0，即函数g（x）在区间（0，+∞）上为增函数，解不等式求出即可．
解答：
解：令g（x）=xf（x）-ln|x|，
则g（x）为偶函数，且当x＞0时，g′（x）＞0，
即函数g（x）在区间（0，+∞）上为增函数，
不等式xf（x）＞1+ln|x|即为g（x）＞g（1），
即有g（|x|）＞g（1），化为|x|＞1，
解得：x＜-1或x＞1．
故选：A．
则g（x）为偶函数，且当x＞0时，g′（x）＞0，
即函数g（x）在区间（0，+∞）上为增函数，
不等式xf（x）＞1+ln|x|即为g（x）＞g（1），
即有g（|x|）＞g（1），化为|x|＞1，
解得：x＜-1或x＞1．
故选：A．
点评：本题考察了函数的单调性，导数的应用，函数的奇偶性，是一道综合题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如果对x＞0，y＞0，有f（x，y）=（x+4y）（
+
）≥m恒成立，那么实数m的取值范围是（ ）
| 2 |
| x |
| 1 |
| 2y |
| A、（-∞，4] |
| B、（8，+∞） |
| C、（-∞，0） |
| D、（-∞，8] |
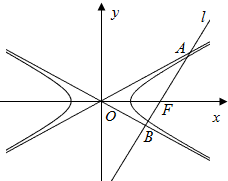如图所示，已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={x|-1＜x＜1}，则下列选项中正确的是（ ）
| A、0⊆A | B、{0}∈A |
| C、∅∈A | D、{0}⊆A |