题目内容
已知动圆过定点P(2,0),且在y轴上截得弦长为4.
(1)求动圆圆心的轨迹Q的方程;
(2)已知点E(m,0)为一个定点,过E作斜率分别为k1、k2的两条直线交轨迹Q于点A、B、C、D四点,且M、N分别是线段AB、CD的中点,若k1+k2=1,求证:直线MN过定点.
(1)求动圆圆心的轨迹Q的方程;
(2)已知点E(m,0)为一个定点,过E作斜率分别为k1、k2的两条直线交轨迹Q于点A、B、C、D四点,且M、N分别是线段AB、CD的中点,若k1+k2=1,求证:直线MN过定点.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设动圆圆心为O1(x,y),动圆与y轴交于R,S两点,由题意,得|O1P|=|O1S|,由此得到
=
,从而能求出动圆圆心的轨迹Q的方程.
(2)由
,得k1y2-4y-4k1m=0,由已知条件推导出M(
+m,
),N(
+m,
),由此能证明直线MN恒过定点(m,2).
| x2+22 |
| (x-2)2+y2 |
(2)由
|
| 2 |
| k12 |
| 2 |
| k1 |
| 2 |
| k22 |
| 2 |
| k2 |
解答:
(1)解:设动圆圆心为O1(x,y),
动圆与y轴交于R,S两点,由题意,得|O1P|=|O1S|,
当O1不在y轴上时,过O1作O1H⊥RS交RS于H,则H是RS的中点,
∴|O1S|=
,
又|O1P|=
,
∴
=
,
化简得y2=4x(x≠0).
又当O1在y轴上时,O1与O重合,
点O1的坐标为(0,0)也满足方程y2=4x,
∴动圆圆心的轨迹Q的方程为y2=4x.
(2)证明:由
,得k1y2-4y-4k1m=0,
y1+y2=
,y1y2=-4m,
AB中点M(
,
),∴M(
+m,
),
同理,点N(
+m,
),
∴kMN=
=
=k1k2,
∴MN:y-
=k1k2[x-(
+m)],
即y=k1k2(x-m)+2,
∴直线MN恒过定点(m,2).
动圆与y轴交于R,S两点,由题意,得|O1P|=|O1S|,
当O1不在y轴上时,过O1作O1H⊥RS交RS于H,则H是RS的中点,
∴|O1S|=
| x2+22 |
又|O1P|=
| (x-2)2+y2 |
∴
| x2+22 |
| (x-2)2+y2 |
化简得y2=4x(x≠0).
又当O1在y轴上时,O1与O重合,
点O1的坐标为(0,0)也满足方程y2=4x,
∴动圆圆心的轨迹Q的方程为y2=4x.
(2)证明:由
|
y1+y2=
| 4 |
| k1 |
AB中点M(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 2 |
| k12 |
| 2 |
| k1 |
同理,点N(
| 2 |
| k22 |
| 2 |
| k2 |
∴kMN=
| yM-yN |
| xM-xN |
| k1k2 |
| k1+k2 |
∴MN:y-
| 2 |
| k1 |
| 2 |
| k12 |
即y=k1k2(x-m)+2,
∴直线MN恒过定点(m,2).
点评:本题考查点的轨迹方程的求法,考查直线过定点的证明,解题时要认真审题,注意中点坐标公式的合理运用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
在极坐标系中,过点(2,
)且垂直于极轴的直线方程为( )
| π |
| 3 |
| A、ρsinθ=-1 |
| B、ρsinθ=1 |
| C、ρcosθ=-1 |
| D、ρcosθ=1 |
函数f(x)是定义域为{x|x≠0}的奇函数,且f(1)=1,f′(x)为f(x)的导函数,当x>0时,f(x)+xf′(x)>
,则不等式xf(x)>1+ln|x|的解集为( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(-∞,-1) |
| C、(1,+∞) |
| D、(-1,1) |
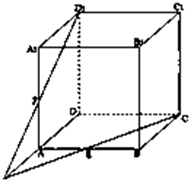 在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.
在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.