题目内容
函数f(x)=x3-x2+ax
(1)a=-1,求f(x)在[0,2]的值域;
(2)f(x)在R上恒增,求a的范围.
(1)a=-1,求f(x)在[0,2]的值域;
(2)f(x)在R上恒增,求a的范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(1)先求出函数的导数,得到单调区间从而求出函数的最值,问题解决,(2)由f′(x)=3x2-2x+a>0,得△=4-12a<0,解出即可.
解答:
解:(1)a=-1时,f(x)=x3-x2-x,
∴f(x)=(3x+1)(x-1),
令f′(x)>0,解得:1<x≤2,
令f′(x)<0,解得:0≤x<1,
∴f(x)在[0,1)递减,在(1,2]递增,
∴f(x)min=f(1)=-1,
而f(0)=0,f(2)=2,
∴f(x)在[0,2]的值域[-1,2];
(2)∵f′(x)=3x2-2x+a,
由f(x)在R上恒增,
∴f′(x)=3x2-2x+a>0,
∴△=4-12a<0,
∴a>
,
故a的范围是:(
,+∞).
∴f(x)=(3x+1)(x-1),
令f′(x)>0,解得:1<x≤2,
令f′(x)<0,解得:0≤x<1,
∴f(x)在[0,1)递减,在(1,2]递增,
∴f(x)min=f(1)=-1,
而f(0)=0,f(2)=2,
∴f(x)在[0,2]的值域[-1,2];
(2)∵f′(x)=3x2-2x+a,
由f(x)在R上恒增,
∴f′(x)=3x2-2x+a>0,
∴△=4-12a<0,
∴a>
| 1 |
| 3 |
故a的范围是:(
| 1 |
| 3 |
点评:本题考察了利用导数研究函数的单调性,函数的最值问题,参数的范围,是一道基础题.

练习册系列答案
相关题目
函数f(x)是定义域为{x|x≠0}的奇函数,且f(1)=1,f′(x)为f(x)的导函数,当x>0时,f(x)+xf′(x)>
,则不等式xf(x)>1+ln|x|的解集为( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(-∞,-1) |
| C、(1,+∞) |
| D、(-1,1) |

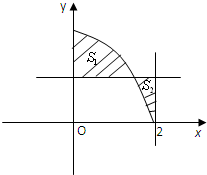 如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).
如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).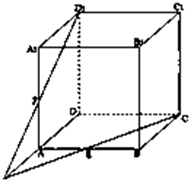 在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.
在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.