题目内容
已知定义在R上的函数y=f(x)存在零点,且对任意m,n∈R都满足f[mf(m)+f(n)]=f2(m)+n.若关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有三个不同的根,则实数a的取值范围是 .
考点:根的存在性及根的个数判断,函数零点的判定定理
专题:函数的性质及应用
分析:令函数y=f(x)的零点为m,即f(m)=0,则由对任意m,n∈R都满足f[mf(m)+f(n)]=f2(m)+n.可得f[f(x)]=x,进而x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有三个不同的根,可转化为|x-3|=1-logax(a>0,a≠1)恰有三个不同的根,根据对数函数的图象和性质分类讨论后,可得答案.
解答:
解:令函数y=f(x)的零点为m,即f(m)=0,
∵对任意m,n∈R都满足f[mf(m)+f(n)]=f2(m)+n.
则f[f(n)]=n恒成立,
即f[f(x)]=x,
若关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有三个不同的根,
即|x-3|=1-logax(a>0,a≠1)恰有三个不同的根,
当0<a<1时,函数y=|x-3|与y=1-logax的图象如下图所示:
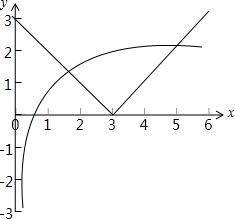
由图可知,函数y=|x-3|与y=1-logax的图象有两个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有两个不同的根,不满足条件;
当1<a<3时,函数y=|x-3|与y=1-logax的图象如下图所示:
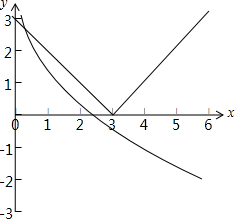
由图可知,函数y=|x-3|与y=1-logax的图象有一个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有一个不同的根,不满足条件;
当a=3时,函数y=|x-3|与y=1-logax的图象如下图所示:
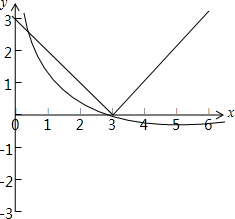
由图可知,函数y=|x-3|与y=1-logax的图象有两个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有两个不同的根,不满足条件;
当a>3时,函数y=|x-3|与y=1-logax的图象如下图所示:

由图可知,函数y=|x-3|与y=1-logax的图象有三个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有三个不同的根,满足条件;
综上所述,实数a的取值范围是(3,+∞),
故答案为:(3,+∞)
∵对任意m,n∈R都满足f[mf(m)+f(n)]=f2(m)+n.
则f[f(n)]=n恒成立,
即f[f(x)]=x,
若关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有三个不同的根,
即|x-3|=1-logax(a>0,a≠1)恰有三个不同的根,
当0<a<1时,函数y=|x-3|与y=1-logax的图象如下图所示:
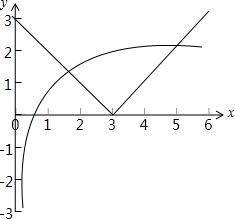
由图可知,函数y=|x-3|与y=1-logax的图象有两个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有两个不同的根,不满足条件;
当1<a<3时,函数y=|x-3|与y=1-logax的图象如下图所示:

由图可知,函数y=|x-3|与y=1-logax的图象有一个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有一个不同的根,不满足条件;
当a=3时,函数y=|x-3|与y=1-logax的图象如下图所示:

由图可知,函数y=|x-3|与y=1-logax的图象有两个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有两个不同的根,不满足条件;
当a>3时,函数y=|x-3|与y=1-logax的图象如下图所示:

由图可知,函数y=|x-3|与y=1-logax的图象有三个交点,即关于x的方程|f[f(x)]-3|=1-logax(a>0,a≠1)恰有三个不同的根,满足条件;
综上所述,实数a的取值范围是(3,+∞),
故答案为:(3,+∞)
点评:本题考查的知识点是根的存在性及根的个数判断,函数零点的判定,其中根据已知确定出f[f(x)]=x,是解答的关键.

练习册系列答案
相关题目
有三个平面α,β,γ,下列命题中正确的是( )
| A、若α,β,γ两两相交,则有三条交线 |
| B、若α⊥β,α⊥γ,则β∥γ |
| C、若α⊥γ,β∩α=a,β∩γ=b,则a⊥b |
| D、若α∥β,β∩γ=∅,则α∩γ=∅ |
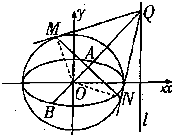 如图,已知椭圆
如图,已知椭圆