题目内容
由于雾霾日趋严重,政府号召市民乘公交出行,但公交车的数量太多会造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的60名候车乘客中进行随机抽样,共抽取10人进行调查反馈,所选乘客情况如表所示:
(1)现从这10人中随机取3人,求至少有一人来自第二组的概率;
(2)现从这10人中随机抽取3人进行问卷调查,设这3个人共来自X个组,求X的分布及数学期望.
| 组别 | 候车时间(单位:min) | 人数 |
| 一 | [0,5) | 1 |
| 二 | [5,10) | 5 |
| 三 | [10,15) | 3 |
| 四 | [15,20) | 1 |
(2)现从这10人中随机抽取3人进行问卷调查,设这3个人共来自X个组,求X的分布及数学期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)设“至少有一人来自第二组”为事件A,利用对立事件概率计算公式能求出至少有一人来自第二组的概率.
(2)由题意A的可能取值为1,2,3,分别求出相应的概率,由此能求出X的分布及数学期望.
(2)由题意A的可能取值为1,2,3,分别求出相应的概率,由此能求出X的分布及数学期望.
解答:
解:(1)设“至少有一人来自第二组”为事件A,
由P(A)=1-
=
.
(2)由题意A的可能取值为1,2,3,
P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
∴X的分布列为:
EX=
(11+2×71+3×38)=
.
由P(A)=1-
| ||
|
| 11 |
| 12 |
(2)由题意A的可能取值为1,2,3,
P(X=1)=
| ||||
|
| 11 |
| 120 |
P(X=2)=
(
| ||||||||||||
|
| 71 |
| 120 |
P(X=3)=
| ||||||||
|
| 38 |
| 120 |
∴X的分布列为:
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 120 |
| 89 |
| 40 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合知识的合理运用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为
某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则其侧视图的面积是( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
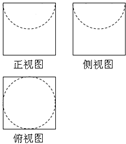 如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是
如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是