题目内容
已知数集A={a1,a2,a3,a4,a5}(0≤a1<a2<a3<a4<a5)具有性质p:对任意i,j∈Z,其中1≤i≤j≤5,均有(aj-ai)∈A,若a5=60,则a3= .
考点:数列的函数特性
专题:等差数列与等比数列
分析:对a1分类讨论,利用性质p:对任意i,j∈Z,其中1≤i≤j≤5,均有(aj-ai)∈A,及其a5=60,即可得出.
解答:
解:①当a1=0时,则a2-a1=a2∈A,a2>0,则a3-a2=a2,∴a3=2a2,同理可得a4=3a2,a5=4a2;由4a2=60,解得a2=15,即A={0,15,30,45,60}.5=∵a5=60,∴a3=30.
②当a1≠0时,同理可得A={12,24,36,48,60},∴a3=36.
②当a1≠0时,同理可得A={12,24,36,48,60},∴a3=36.
点评:本题考查了满足某种性质的数列、集合的求法,考查了分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线
-y2=1的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值是( )
| x2 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
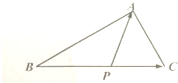 如图,已知△ABC中,A=90°,B=30°,点P在BC上运动且满足
如图,已知△ABC中,A=90°,B=30°,点P在BC上运动且满足| CP |
| CB |
| PA |
| PC |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=
x3-
x2+
x+1在x=1处的切线的倾斜角为α,则
的值是( )
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| cos2α |
| sin2α-cos2α |
A、
| ||
B、
| ||
C、-
| ||
D、-
|