题目内容
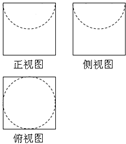如图是一个无盖器皿的三视图，正视图、侧视图和俯视图 中的正方形边长为2，正视图、侧视图中的虚线都是半圆，则该器皿的表面积是考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：该器皿的表面积可分为两部分：去掉一个圆的正方体的表面积s1和半球的表面积s2，即可求出该器皿的表面积．
解答：
解：该器皿的表面积可分为两部分：去掉一个圆的正方体的表面积s1和半球的表面积s2，s1=6×2×2-π×12=24-π，s2=
×4π×12=2π，
故s=s1+s2=π+24
故答案为：π+24．
| 1 |
| 2 |
故s=s1+s2=π+24
故答案为：π+24．
点评：由三视图求表面积与体积，关键是正确分析原图形的几何特征．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知某个多面体的三视图（单位cm）如图所示，则此多面体的体积是已知全集U=R，A={x|x≤a+2}，B={x|x≥a2}，若∁U（A∩B）=R，则a的取值范围是（ ）
| A、[-1，2] |
| B、（-1，2） |
| C、（-∞，-1]∪[2，+∞） |
| D、（-∞，-1）∪（2，+∞） |
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=AD=2，四边形ABCD满足AB⊥AD，BC∥AD且BC=4，点M为PC中点，点E为BC边上的动点，且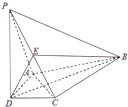
如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AD⊥DC，DB平分∠ADC，E为PC的中点，AD=CD=1，DB=2