题目内容
以坐标原点为极点,以x轴的非负半轴为极轴建立极坐标系,已知曲线C的参数方程为
(t为参数).
(1)曲线C在点(1,1)处的切线为l,求l的极坐标方程;
(2)点A的极坐标为(2
,
),且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
|
(1)曲线C在点(1,1)处的切线为l,求l的极坐标方程;
(2)点A的极坐标为(2
| 2 |
| π |
| 4 |
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:导数的综合应用
分析:(1)化简参数方程为普通方程,判断曲线C与点(1,1)的位置关系,求出切线的普通方程,然后化为l的极坐标方程;
(2)设出够点A的极坐标为(2
,
),参数t∈[0,π]时的直线方程,判断直线与圆的位置关系,通过相切,求直线m的斜率的取值范围.
(2)设出够点A的极坐标为(2
| 2 |
| π |
| 4 |
解答:
 解:(Ⅰ)
解:(Ⅰ)
,∴x2+y2=2,
点C(1,1)在圆上,
故切线l方程为x+y=2…(2分)
∴ρsinθ+ρcosθ=2,
切线l的极坐标方程:ρsin(θ+
)=
…(5分)
(Ⅱ)y=k(x-2)+2与半圆x2+y2=2(y≥0)相切时
=
∴k2-4k+1=0,∴k=2-
,k=2+
(舍去)….(8分)
设点B(-
,0),KAB=
=2-
,
故直线m的斜率的取值范围为(2-
,2-
].…(10分)
 解:(Ⅰ)
解:(Ⅰ)
|
点C(1,1)在圆上,
故切线l方程为x+y=2…(2分)
∴ρsinθ+ρcosθ=2,
切线l的极坐标方程:ρsin(θ+
| π |
| 4 |
| 2 |
(Ⅱ)y=k(x-2)+2与半圆x2+y2=2(y≥0)相切时
| |2k-2| | ||
|
| 2 |
∴k2-4k+1=0,∴k=2-
| 3 |
| 3 |
设点B(-
| 2 |
| 2-0 | ||
2+
|
| 2 |
故直线m的斜率的取值范围为(2-
| 3 |
| 2 |
点评:本题考查直线与圆的位置关系,极坐标方程以及参数方程的求法与应用,考查分析问题解决问题的能力.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 某校为了解高一学生12月份的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在[8,12]小时内的人数为
某校为了解高一学生12月份的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在[8,12]小时内的人数为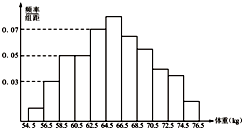 为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17.5岁到18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这200名学生中体重在[56.5,64.5]的学生人数是
为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17.5岁到18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这200名学生中体重在[56.5,64.5]的学生人数是