Question

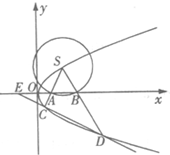如图，S（1，1）是抛物线为y²=2px（p＞0）上的一点，以S为圆心，r为半径（1＜r＜

2

）做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点．
（Ⅰ）求证：直线CD的斜率为定值；
（Ⅱ）延长DC交x轴负半轴于点E，若EC：ED=1：3，求sin2∠CSD+cos∠CSD的值．

Answer 1

考点：余弦定理,直线的斜率

专题：三角函数的求值

分析：（Ⅰ）将S坐标代入抛物线解析式求出p的值，确定出抛物线解析式，设直线SA的方程为y-1=k（x-1），C（x₁，y₁），与抛物线方程y²=x联立，消去x得到关于y的一元二次方程，利用韦达定理表示出y₁，进而表示出x₁，即C坐标，由SA=SB，得到直线SB的斜率与直线SA斜率互为相反数，表示出直线CD斜率，化简得到结果为常数；
求证：直线CD的斜率为定值；
（Ⅱ）设E（t，0），根据题意得到

EC

=

1

3

ED

，将各自坐标代入求出k的值，确定出A与B坐标，进而求出cos∠CSD的值，确定出sin∠SCD的值，求出sin2∠CSD的值，代入原式计算即可得到结果．

解答： 解：（Ⅰ）将点（1，1）代入y²=2px，得2p=1，即p=

1

2

，
∴抛物线方程为y²=x，
设直线SA的方程为y-1=k（x-1），C（x₁，y₁），
与抛物线方程y²=x联立，消去x得：ky²-y+1-k=0，
∴y₁+1=

1

k

，即y₁=

1

k

-1，
∴C（

(1-k)2

k2

，

1

k

-1），
∵SA=SB，
∴直线SB的斜率为-k，
∴k_CD=

1 k -1+ 1 k +1

(1-k)2 k2 - (1+k)2 k2

=-

1

2

；                                           
（Ⅱ）设E（t，0），
∵

EC

=

1

3

ED

，
∴（

(1-k)2

k2

-t，

1

k

-1）=

1

3

（

(1+k)2

k2

-t，-

1

k

-1），即

1

k

-1=

1

3

（-

1

k

-1），
解得：k=2，
∴直线SA的方程为y=2x-1，
∴A（

1

2

，0），
同理B（

3

2

，0），
∴cos∠CSD=cos∠ASB=

SA2+SB2-AB2

2SB•SA

=

3

5

，
∴sin∠CSD=

1-( 3 5 )2

=

4

5

，
∴sin2∠CSD=2sin∠CSDcos∠CSD=

24

25

，
则sin2∠CSD+cos∠CSD=

39

25

．

点评：此题考查了余弦定理，平面向量的数量积运算，同角三角函数间的基本关系，二倍角的正弦函数公式，以及直线的斜率，熟练掌握定理及公式是解本题的关键．