题目内容
已知函数f（x）=（asinx+bcosx）•e-x在x=
处有极值，则函数y=asinx+bcosx的图象可能是（ ）
| π |
| 6 |
A、 |
B、 |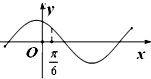
C、 |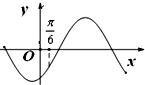
D、 |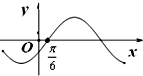
考点：函数的图象
专题：函数的性质及应用,导数的综合应用
分析：先对f（x）求导，再利用极值的性质求出a，b的关系式，代入y=asinx+bcosx，再利用函数的性质（特殊点、单调性等）进行筛选．
解答：
解：∵f′（x）=（acosx-bsinx）•e-x-（asinx+bcosx）•e-x=e-x[（a-b）cosx-（a+b）sinx]，
又∵f（x）=（asinx+bcosx）•e-x在x=
处有极值，∴f′(
)=e-
[(a-b)cos
-(a+b)sin
]=0，
整理得a=
b，代入y=asinx+bcosx后得y=b[(2+
)sinx+cosx]①，∴y′=b[（2+
）cosx-sinx]②，
对于A项，∵f（0）＜0，所以b＜0，此时将x=
分别代入①②，经计算f（
）＜0，f′(
)＜0，与图象相符，所以A选项符合题意；
对于B项，∵f（0）＞0，所以b＞0，此时将x=
分别代入①②，经计算f′(
)＞0，与图象在x=
处是减函数不符，所以B选项不符合题意；
对于C项，∵f（0）＜0，所以b＜0，此时将x=
分别代入①②，经计算f′(
)＜0，与图象在x=
处是增函数不符，所以C选项不符合题意；
对于D项，∵f（0）＜0，所以b＜0，此时将x=
代入①，经计算f（
）＜0，与图象不符，所以D选项不符合题意．
故选A
又∵f（x）=（asinx+bcosx）•e-x在x=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
整理得a=
1+
| ||
|
| 3 |
| 3 |
对于A项，∵f（0）＜0，所以b＜0，此时将x=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
对于B项，∵f（0）＞0，所以b＞0，此时将x=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
对于C项，∵f（0）＜0，所以b＜0，此时将x=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
对于D项，∵f（0）＜0，所以b＜0，此时将x=
| π |
| 6 |
| π |
| 6 |
故选A
点评：由函数式确定图象的问题，一般从函数的性质（定义域、值域、单调性、奇偶性、对称性、周期、渐近线等）分析入手，注意结合特殊点、极值点的应用．
练习册系列答案
相关题目
给出如下四个命题：
①若“p∨q”为真命题，则p、q均为真命题；
②“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”；
③“?x∈R，x2+x≥1”的否定是“?x0∈R，x02+x0≤1”；
④“x＞0”是“x+
≥2”的充要条件．
其中不正确的命题是（ ）
①若“p∨q”为真命题，则p、q均为真命题；
②“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”；
③“?x∈R，x2+x≥1”的否定是“?x0∈R，x02+x0≤1”；
④“x＞0”是“x+
| 1 |
| x |
其中不正确的命题是（ ）
| A、①② | B、②③ | C、①③ | D、③④ |
在数列{an}中，a1=1，a2=
，且
+
=
（n≥3，n∈N*），则a4=（ ）
| 2 |
| 3 |
| 1 |
| an-2 |
| 1 |
| an |
| 2 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
设函数f（x）=x2-2ax+b（a，b∈R），则“f（x）=0在区间[1，2]有两个不同的实根”是“1＜a＜2”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若对定义在R上的可导函数f（x）恒有（4-x）f（x）+xf′（x）＞0，则f（x）（ ）
| A、恒大于等于0 |
| B、恒小于0 |
| C、恒大于0 |
| D、和0的大小关系不能确定 |
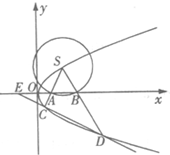如图，S（1，1）是抛物线为y2=2px（p＞0）上的一点，以S为圆心，r为半径（1＜r＜