题目内容
已知公差不为0的等差数列{an}的首项a1=2,且
,
,
成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+2b2+22b3+…+2n-1bn=an,求数列{nbn}的前n项和Tn.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+2b2+22b3+…+2n-1bn=an,求数列{nbn}的前n项和Tn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)利用等比数列的性质列出方程求得公比,即可得出结论;
(2)利用错位相减法求得数列的和即可.
(2)利用错位相减法求得数列的和即可.
解答:
解:(1)设等差数列{an}的公差为d,
由(
)2=
•
,得(a1+d)2=a1(a1+3d).
因为d≠0,所以d=a1=2,
所以an=2n.(4分)
(2)b1+2b2+4b3+…+2n-1bn=an①
b1+2b2+4b3+…+2n-1bn+2nbn+1=an+1②
②-①得:2n•bn+1=2.
∴bn+1=21-n.
当n=1时,b1=a1=2,∴bn=22-n.(8分)
Tn=
+
+
+…+
,
Tn=
+
+
+…+
,上两式相减得
Tn=2+
+
+
+…+
-
=2+2•(1-
)-
,
∴Tn=8-
.(12分)
由(
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| a4 |
因为d≠0,所以d=a1=2,
所以an=2n.(4分)
(2)b1+2b2+4b3+…+2n-1bn=an①
b1+2b2+4b3+…+2n-1bn+2nbn+1=an+1②
②-①得:2n•bn+1=2.
∴bn+1=21-n.
当n=1时,b1=a1=2,∴bn=22-n.(8分)
Tn=
| 1 |
| 2-1 |
| 2 |
| 20 |
| 3 |
| 21 |
| n |
| 2n-2 |
| 1 |
| 2 |
| 1 |
| 20 |
| 2 |
| 21 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
| n |
| 2n-1 |
| 1 |
| 2n-1 |
| n |
| 2n-1 |
∴Tn=8-
| n+2 |
| 2n-2 |
点评:本题主要考查等比数列的性质及数列求和的方法错位相减法知识,考查学生的运算求解能力,属中档题.

练习册系列答案
相关题目
设函数f(x)=x2-2ax+b(a,b∈R),则“f(x)=0在区间[1,2]有两个不同的实根”是“1<a<2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
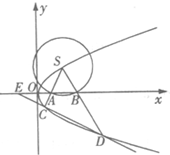 如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r<
如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r<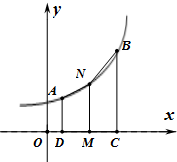 已知函数f(x)=lnx.
已知函数f(x)=lnx.