题目内容
|1-x|+|x-5|≤4解集为 ．
考点：绝对值不等式的解法
专题：选作题,不等式
分析：求出两个绝对值内的零点，然后由零点进行分段，去绝对值后求解一次不等式，最后取并集．
解答：
解：当x＜1时，不等式|1-x|+|x-5|≤4化为：-（x-1）-（x-5）≤4，
即-2x≤10，则x≥-5，所以，x的范围是-5≤x＜1；
当-1≤x≤5时，不等式|1-x|+|x-5|≤4化为：（x-1）-（x-5）≤4，即4≤4，此不等式恒成立；
当x＞5时，不等式|1-x|+|x-5|≤4化为：x-1+x-5≤4，即2x≤10，则x≤5．无解．
综上，不等式|1-x|+|x-5|≤4的解集为[-5，5]．
故答案为：[-5，5]．
即-2x≤10，则x≥-5，所以，x的范围是-5≤x＜1；
当-1≤x≤5时，不等式|1-x|+|x-5|≤4化为：（x-1）-（x-5）≤4，即4≤4，此不等式恒成立；
当x＞5时，不等式|1-x|+|x-5|≤4化为：x-1+x-5≤4，即2x≤10，则x≤5．无解．
综上，不等式|1-x|+|x-5|≤4的解集为[-5，5]．
故答案为：[-5，5]．
点评：本题考查了绝对值不等式的解法，考查了不等式的分段问题，分段求解后取并集得原不等式的解集，此题是中档题．
练习册系列答案
阅读快车系列答案
相关题目
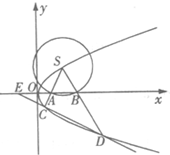如图，S（1，1）是抛物线为y2=2px（p＞0）上的一点，以S为圆心，r为半径（1＜r＜