题目内容
 近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.
近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.(1)求该组织的人数;
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,用列举法求出第3组至少有一名志愿者被抽中的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)根据频数=频率×样本容量,频率=对应矩形面积,构造关于n的方程,解方程可得该组织的人数;
(2)先计算出第3,4,5组中每组的人数,进而根据比例,可得到应从第3,4,5组各抽取多少名志愿者;
(3)选求出这6名志愿者中随机抽取2名志愿者的基本事件总数和第3组至少有一名志愿者被抽中的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)先计算出第3,4,5组中每组的人数,进而根据比例,可得到应从第3,4,5组各抽取多少名志愿者;
(3)选求出这6名志愿者中随机抽取2名志愿者的基本事件总数和第3组至少有一名志愿者被抽中的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)由题意:第2组的人数:35=5×0.07•n,得到:n=100,
故该组织有100人.…(3分)
(2)第3组的人数为0.3×100=30,
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10.
∵第3,4,5组共有60名志愿者,
∴利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:
第3组:
×6=3; 第4组:
×6=2; 第5组:
×6=1.
∴应从第3,4,5组中分别抽取3人,2人,1人.…(6分)
(3)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1B2,第5组的1名志愿者为C1.则从6名志愿者中抽取2名志愿者有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),
(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),
(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.
其中第3组的3名志愿者A1,A2,A3,至少有一名志愿者被抽中的有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),
(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),共有12种,
则第3组至少有一名志愿者被抽中的概率为p=
=
. …(12分)
故该组织有100人.…(3分)
(2)第3组的人数为0.3×100=30,
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10.
∵第3,4,5组共有60名志愿者,
∴利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:
第3组:
| 30 |
| 60 |
| 20 |
| 60 |
| 10 |
| 60 |
∴应从第3,4,5组中分别抽取3人,2人,1人.…(6分)
(3)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1B2,第5组的1名志愿者为C1.则从6名志愿者中抽取2名志愿者有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),
(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),
(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.
其中第3组的3名志愿者A1,A2,A3,至少有一名志愿者被抽中的有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),
(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),共有12种,
则第3组至少有一名志愿者被抽中的概率为p=
| 12 |
| 15 |
| 4 |
| 5 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
积分∫
dx=( )
0 |
| cos2x |
| cosx+sinx |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
若对定义在R上的可导函数f(x)恒有(4-x)f(x)+xf′(x)>0,则f(x)( )
| A、恒大于等于0 |
| B、恒小于0 |
| C、恒大于0 |
| D、和0的大小关系不能确定 |
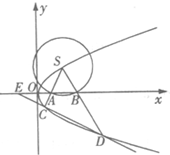 如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r<
如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r< 如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=
如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=