题目内容
已知A={x|-2≤x≤5}，B={x|m+1≤
x≤2m-1}，B⊆A，求m的取值范围．
| 1 |
| 2 |
考点：集合的包含关系判断及应用
专题：集合
分析：本题是一元一次不等式和集合包含关系结合的题目，需要对m分类讨论，考虑集合B为空集的情况．
解答：
解：∵B={x|m+1≤
x≤2m-1}，
即B={x|2m+2≤x≤4m-2}，又B⊆A，
∴①当B=∅时，2m+2＞4m-2，解得m＜2；
②当B≠∅时，即m≥2时，
只需满足不等式组
，
解得：-2≤m≤
，又m≥2，故此时B=∅；
综上所述，m＜2．
| 1 |
| 2 |
即B={x|2m+2≤x≤4m-2}，又B⊆A，
∴①当B=∅时，2m+2＞4m-2，解得m＜2；
②当B≠∅时，即m≥2时，
只需满足不等式组
|
解得：-2≤m≤
| 7 |
| 4 |
综上所述，m＜2．
点评：本题主要考查集合的包含基本运算，属于基础题．要正确判断两个集合间的关系，必须对集合的相关概念有深刻的理解，善于抓住代表元素，认清集合的特征．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
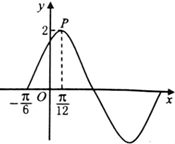已知函数f（x）=Asin（ωx+φ），（ω＞0，A＞0，φ∈（0，
