题目内容
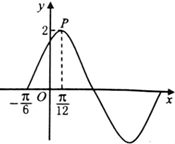 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,| π |
| 2 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)已知α∈(π,
| 3π |
| 2 |
| α |
| 2 |
| 5π |
| 12 |
| 12 |
| 13 |
| α |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(Ⅰ)由函数f(x)=Asin(ωx+φ)的图象易知A=2,T=π,从而可求得ω=2;由ω•
+φ=2kπ+
,k∈Z,及φ∈(0,
)可求得φ=
,于是可得函数f(x)的解析式;
(Ⅱ)化简f(
-
)=-cosα,依题意知cosα=-
,α∈(π,
),易求sinα=-
,从而可求得f(
)=2sin(2×
+
)的值.
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
(Ⅱ)化简f(
| α |
| 2 |
| 5π |
| 12 |
| 6 |
| 13 |
| 3π |
| 2 |
| ||
| 13 |
| α |
| 2 |
| α |
| 2 |
| π |
| 3 |
解答:
解:(Ⅰ)由图知,A=2,T=4[
-(-
)]=π,
由
=π,得ω=2;
又ω•
+φ=2kπ+
,k∈Z,及φ∈(0,
)得φ=
,
∴f(x)=2sin(2x+
);
(Ⅱ)∵f(
-
)=2sin[2(
-
)+
]=2sin(α-
)=-2cosα=
,
∴cosα=-
,又由α∈(π,
)知,sinα<0,
∴sinα=-
=-
=-
,
∴f(
)=2sin(2×
+
)=2(sinαcos
+cosαsin
)
=2(-
×
-
×
)
=-
.
| π |
| 12 |
| π |
| 6 |
由
| 2π |
| ω |
又ω•
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
∴f(x)=2sin(2x+
| π |
| 3 |
(Ⅱ)∵f(
| α |
| 2 |
| 5π |
| 12 |
| α |
| 2 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| 12 |
| 13 |
∴cosα=-
| 6 |
| 13 |
| 3π |
| 2 |
∴sinα=-
| 1-cos2α |
1-(-
|
| ||
| 13 |
∴f(
| α |
| 2 |
| α |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=2(-
| ||
| 13 |
| 1 |
| 2 |
| 6 |
| 13 |
| ||
| 2 |
=-
| ||||
| 13 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查诱导公式与两角和的余弦的应用,考查转化思想与运算求解能力,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
设函数f(x)可导,则
等于( )
| lim |
| △x→0 |
| f(15+3△x)-f(15) |
| △x |
| A、f′(15) | ||
| B、3f′(15) | ||
C、
| ||
| D、f′(3) |
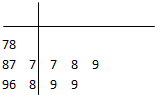 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):