题目内容
已知平面向量
=(3,4),
=(9,x),
=(4,y),
∥
,
⊥
.
(1)求
和
;
(2)若
=2
-
,
=
+c,求向量
、
夹角的大小.
| a |
| b |
| c |
| a |
| b |
| a |
| c |
(1)求
| a |
| b |
(2)若
| m |
| a |
| b |
| n |
| a |
| m |
| n |
考点:平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:(1)根据向量平行和垂直的坐标公式即可得到结论.
(2)求出向量
、
,利用数量积的应用,即可得到结论.
(2)求出向量
| m |
| n |
解答:
解(1)∵
∥
,
⊥
.
∴若
∥
,
⊥
.
则3x-4×9=0,3×4+4y=0,
解得x=12,y=-3,
∴
=(3,4),
=(9,12),
=(4,-3).
(2)则
=2
-
=(-3,-4),
=
+c=(7,1),
故|
|=5,|
|=5
,
•
=(-3,-4)•(7,1)=-25,
∴向量
、
夹角的大小为cosθ=
=
=-
,
∴向量
、
夹角为
.
| a |
| b |
| a |
| b |
∴若
| a |
| b |
| a |
| c |
则3x-4×9=0,3×4+4y=0,
解得x=12,y=-3,
∴
| a |
| b |
| c |
(2)则
| m |
| a |
| b |
| n |
| a |
故|
| m |
| n |
| 2 |
| m |
| n |
∴向量
| m |
| n |
| ||||
|
|
| -25 | ||
5×5
|
| ||
| 2 |
∴向量
| m |
| n |
| 3π |
| 4 |
点评:本题主要考查平面向量的基本运算,要求熟练掌握平面向量的数量积公式.

练习册系列答案
相关题目
由点P(4,3)引圆x2+y2=9的切线,则切线的长为( )
| A、5 | B、4 | C、3 | D、2 |
设函数f(x)可导,则
等于( )
| lim |
| △x→0 |
| f(15+3△x)-f(15) |
| △x |
| A、f′(15) | ||
| B、3f′(15) | ||
C、
| ||
| D、f′(3) |
已知函数y=f(2x)+x是偶函数,且f(2)=1,则f(-2)=( )
| A、2 | B、3 | C、4 | D、5 |
下列不等式成立的是( )
| A、ex<x+1 | ||||
| B、lnx>x-1 | ||||
C、sinx<
| ||||
D、sinx>
|
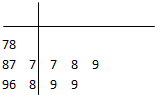 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):