Question

已知f（x）是定义在R上的奇函数，且f（x+2）=-f　（x），当0≤x≤1时，f（x）=x．
（1）求f（π）的值；
（2）当-4≤x≤4时，求f（x）的图象与x轴围成图形的面积．
（3）求函数f（x）的解析式及单调区间．（不必写推导过程）

Answer 1

考点：函数奇偶性的性质,函数解析式的求解及常用方法,函数的周期性

专题：函数的性质及应用

分析：（1）由f（x+2）=-f　（x），可得f（x+4）=-f（x+2）=f（x），即函数f（x）是周期为4的函数．可得f（π）=f（π-4），利用f（x）是定义在R上的奇函数，可得f（π）=-f（4-π）．由于当0≤x≤1时，f（x）=x．即可得出．
（2）设-1≤x≤0，则0≤-x≤1．当0≤x≤1时，f（x）=x，f（x）是定义在R上的奇函数，可得f（x）=-f（-x）=-（-x）=x．令1≤x≤3，可得-1≤x-2≤1，
又f（x+2）=-f　（x），可得f（x）=-f（x-2）=-（x-2）=-x+2．再利用函数的周期性同理可得：f（x）=

x+4，-4≤x＜-3 -x-2，-3≤x＜-1 x，-1≤x≤1 -x+2，1＜x≤3 x-4，3＜x≤4

函数f（x）的图象如图所示，利用三角形的面积计算公式与x轴围成图形的面积即可得出．
（3）由（2）及其函数的奇偶性与周期性即可得出．

解答： 解：（1）∵f（x+2）=-f　（x），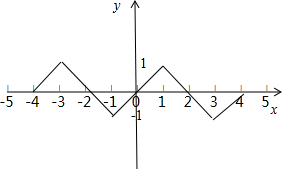
∴f（x+4）=-f（x+2）=f（x），
∴函数f（x）是周期为4的函数．
∴f（π）=f（π-4），
∵f（x）是定义在R上的奇函数，
∴f（π-4）=-f（4-π），
∴f（π）=-f（4-π）．
当0≤x≤1时，f（x）=x．
∴f（π）=-f（4-π）=-（4-π）=π-4．
（2）设-1≤x≤0，则0≤-x≤1．
∵当0≤x≤1时，f（x）=x，f（x）是定义在R上的奇函数，
∴f（x）=-f（-x）=-（-x）=x．
令1≤x≤3，
则-1≤x-2≤1，
又f（x+2）=-f　（x），
∴f（x）=-f（x-2）=-（x-2）=-x+2．
再利用函数的周期性同理可得：3≤x≤4，f（x）=x-4．
-4≤x≤-3，f（x）=x+4；
-3≤x≤-1，f（x）=-x-2．
∴f（x）=

x+4，-4≤x＜-3 -x-2，-3≤x＜-1 x，-1≤x≤1 -x+2，1＜x≤3 x-4，3＜x≤4

函数f（x）的图象如图所示，
与x轴围成图形的面积S=

1

2

×2×1×4=4．
（3）由（2）可得：
f（x）=

(-1)k(x+2k)，x∈(-2k-1，-2k+1] x，x∈[-1，1] (-1)kx+(-1)k+12k，x∈(2k-1，2k+1]

．

点评：本题考查了考查了函数的奇偶性、周期性及其图象与性质，考查了推理能力与计算能力，考查了数形结合的思想方法，属于难题．