题目内容
探照灯反射镜的轴截面是抛物线y2=2px(x>0)的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60cm,灯深40cm,则抛物线的焦点坐标为( )
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:依题意可知点(40,30)在抛物线上,代入抛物线方程得302=80p,求出p,即可求出抛物线的焦点坐标.
解答:
解:由题意,抛物线方程为y2=2px
依题意可知点(40,30)在抛物线上,代入抛物线方程得302=80p
解得p=
,
∴抛物线的焦点坐标为(
,0),
故选:C,
依题意可知点(40,30)在抛物线上,代入抛物线方程得302=80p
解得p=
| 45 |
| 4 |
∴抛物线的焦点坐标为(
| 45 |
| 4 |
故选:C,
点评:本题考查抛物线方程的求法与性质,是基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
集合A={x|1<x<2},集合B={x|x>1},则A∩B=( )
| A、(-∞,-1)∪(1,2) |
| B、(1,+∞) |
| C、(1,2) |
| D、[2,+∞) |
与椭圆
+
=1共焦点,且与双曲线
-y2=1有相同渐近线的双曲线方程是( )
| x2 |
| 64 |
| y2 |
| 100 |
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
点M与点F(3,0)的距离比它到直线x+5=0的距离小2,则点M的轨迹方程为( )
| A、y2=-12x |
| B、y2=6x |
| C、y2=12x |
| D、y2=-6x |
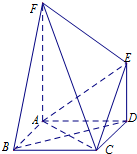 如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.
如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.