题目内容
已知椭圆中心在原点,焦点在x轴上,椭圆短轴的一个顶点B与两个焦点F1,F2组成的△BF1F2的周长为4+2
,且∠BF1F2=45°,求这个椭圆的方程.
| 2 |
考点:椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出椭圆方程,根据条件可得△BF1F2为等腰直角三角形,则b=c,a=
c,由△BF1F2的周长得到c的方程,解得c,可得a,b,进而得到椭圆方程.
| 2 |
解答:
解:设椭圆方程为
+
=1(a>b>0),
|F1F2|=2c,|BF1|=|BF2|=a,
由于∠BF1F2=45°,则△BF1F2为等腰直角三角形,
则b=c,a=
c,
则△BF1F2的周长为2a+2c=2
c+2c=4+2
,
解得,c=
,
则有a=2,b=
,
则椭圆方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
|F1F2|=2c,|BF1|=|BF2|=a,
由于∠BF1F2=45°,则△BF1F2为等腰直角三角形,
则b=c,a=
| 2 |
则△BF1F2的周长为2a+2c=2
| 2 |
| 2 |
解得,c=
| 2 |
则有a=2,b=
| 2 |
则椭圆方程为
| x2 |
| 4 |
| y2 |
| 2 |
点评:本题考查椭圆的方程、定义和性质,考查运算能力,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
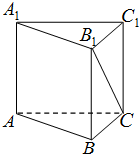 如图,正三棱柱的底面边长为2,体积为
如图,正三棱柱的底面边长为2,体积为 如图⊙O的直径为CA,OB⊥CA,M在OA上,连接BM交⊙O于N,以N为切点,作⊙O的切线交CA延长线于P.
如图⊙O的直径为CA,OB⊥CA,M在OA上,连接BM交⊙O于N,以N为切点,作⊙O的切线交CA延长线于P.