题目内容
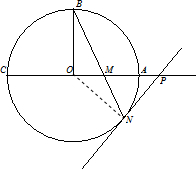
如图⊙O的直径为CA，OB⊥CA，M在OA上，连接BM交⊙O于N，以N为切点，作⊙O的切线交CA延长线于P．（Ⅰ）求证PM=PN；
（Ⅱ）若⊙O的半径为2，PM=
| 5 |
考点：与圆有关的比例线段
专题：立体几何
分析：（Ⅰ）连接ON，根据切线的性质可得ON⊥PN，由同角的余角相等，可得∠PMN=∠PNM，进而得到PM=PN；
（Ⅱ）：（Ⅱ）设AM=x，则PA=
-x，PC=4+
-x，根据PM=PN=
，结合切割线定理，构造关于x的方程，解方程，可得AM的长．
（Ⅱ）：（Ⅱ）设AM=x，则PA=
| 5 |
| 5 |
| 5 |
解答：
证明：（Ⅰ）连接ON，
∵PN与圆O相切，N为切点，
∴ON⊥PN，
故∠PNM+∠ONM=90°，
又∵OB⊥CA，
∴∠OMB+∠OBM=90°，
又∵∠OBM=∠ONM，
∴∠OMB=∠PNM，即∠PMN=∠PNM，
∴PM=PN；
解：（Ⅱ）设AM=x，
∵⊙O的半径为2，PM=PN=
，
∴PA=
-x，PC=4+
-x，
由切割线定理可得：PN2=PA•PB，
即5=（
-x）（4+
-x），
解得x=
-1，或x=
+5（舍），
故AM=
-1
∵PN与圆O相切，N为切点，
∴ON⊥PN，
故∠PNM+∠ONM=90°，
又∵OB⊥CA，
∴∠OMB+∠OBM=90°，
又∵∠OBM=∠ONM，
∴∠OMB=∠PNM，即∠PMN=∠PNM，
∴PM=PN；
解：（Ⅱ）设AM=x，
∵⊙O的半径为2，PM=PN=
| 5 |
∴PA=
| 5 |
| 5 |
由切割线定理可得：PN2=PA•PB，
即5=（
| 5 |
| 5 |
解得x=
| 5 |
| 5 |
故AM=
| 5 |
点评：本题考查的知识点是切线的性质，切割线定理，难度不大，属于基础题．
练习册系列答案
相关题目
椭圆
+
=1中，以点M（-1，2）为中点的弦所在的直线斜率为（ ）
| x2 |
| 16 |
| y2 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
过双曲线
-x2=1的下焦点F作抛物线C：x2=2py（p＞0）的两条切线，切点分别为AB，若FA⊥FB，则抛物线的方程为（ ）
| y2 |
| 3 |
| A、x2=2y |
| B、x2=4y |
| C、x2=6y |
| D、x2=8y |
已知a，b∈[-2，2]，在此范围内任取数对（a，b），能使函数f（x）=x3-3x+a+b，有三个不同零点的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|