题目内容
已知过点P(1,2)的直线l,被双曲线2x2-y2=2截得的弦AB长4
,求直线l的方程.
| 2 |
考点:双曲线的简单性质
专题:计算题,作图题,圆锥曲线的定义、性质与方程
分析:由题意作图,设直线l的方程为y=k(x-1)+2,从而可得(2-k2)x2+(2k2-4k)x-k2+4k-6=0,从而可得m+n=-
,m•n=
;利用弦长公式可得2k4+2k3-11k2+2k+5=0,从而解得k=1,从而写出直线的方程即可.
| 2k2-4k |
| 2-k2 |
| -k2+4k-6 |
| 2-k2 |
解答:
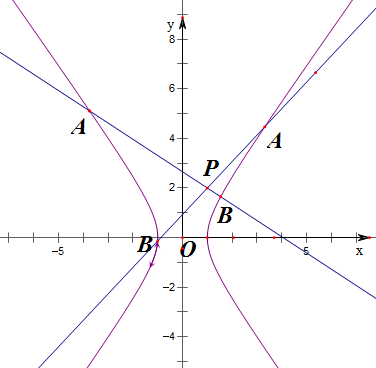 解:作图如右图,
解:作图如右图,
设直线l的方程为y=k(x-1)+2,
与双曲线方程2x2-y2=2联立消y得,
(2-k2)x2+(2k2-4k)x-k2+4k-6=0,
设A(m,k(m-1)+2),B(n,k(n-1)+2);
故m+n=-
,m•n=
;
则由弦AB长4
可得,
•|m-n|=4
,
即(1+k2)[(-
)2-4
]=32,
化简可得,2k4+2k3-11k2+2k+5=0,
解得,k=1;
故直线l的方程为y=x+1.
 解:作图如右图,
解:作图如右图,设直线l的方程为y=k(x-1)+2,
与双曲线方程2x2-y2=2联立消y得,
(2-k2)x2+(2k2-4k)x-k2+4k-6=0,
设A(m,k(m-1)+2),B(n,k(n-1)+2);
故m+n=-
| 2k2-4k |
| 2-k2 |
| -k2+4k-6 |
| 2-k2 |
则由弦AB长4
| 2 |
| 1+k2 |
| 2 |
即(1+k2)[(-
| 2k2-4k |
| 2-k2 |
| -k2+4k-6 |
| 2-k2 |
化简可得,2k4+2k3-11k2+2k+5=0,
解得,k=1;
故直线l的方程为y=x+1.
点评:本题考查了圆锥曲线的应用及运算化简能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
椭圆
+
=1中,以点M(-1,2)为中点的弦所在的直线斜率为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
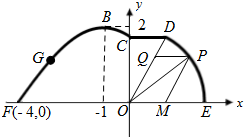 如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧