题目内容
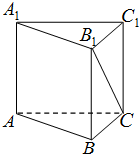如图，正三棱柱的底面边长为2，体积为| 3 |
考点：直线与平面所成的角
专题：空间位置关系与距离
分析：首先利用则正三棱柱的体积公式先求出高，进一步先确定直线与平面的夹角，最后解直角三角形求得线面的夹角．
解答：
解：已知：正三棱柱的底面边长为2，体积为
．
则：设正三棱柱的高为h
所以：利用V=S△ABC•h
解得：h=1
直线B1C与底面ABC所成的角为∠B1CB
则：tan∠B1CB=
=
直线B1C与底面ABC所成的角：arctan
故答案为：arctan
| 3 |
则：设正三棱柱的高为h
所以：利用V=S△ABC•h
解得：h=1
直线B1C与底面ABC所成的角为∠B1CB
则：tan∠B1CB=
| BB1 |
| BC |
| 1 |
| 2 |
直线B1C与底面ABC所成的角：arctan
| 1 |
| 2 |
故答案为：arctan
| 1 |
| 2 |
点评：本题考查的知识要点：棱柱的体积运算，直线与平面的夹角的应用．属于基础题型．
练习册系列答案
相关题目
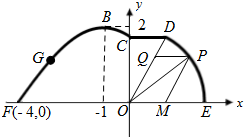如图，在海岸线EF一侧有一休闲游乐场，游乐场的前一部分边界为曲线段FGBC，该曲线段是函数y=Asin（ωx+ϕ）（A＞0，ω＞0，ϕ∈（0，π）），x∈[-4，0]的图象，图象的最高点为B（-1，2）．边界的中间部分为长1千米的直线段CD，且CD∥EF．游乐场的后一部分边界是以O为圆心的一段圆弧
下列结论正确的是（ ）
A、若向量
| ||||||||||||
B、已知向量
| ||||||||||||
C、“若 θ=
| ||||||||||||
| D、若命题 p：?x∈R，x2-x+1＜0，则?p：?x∈R，x2-x+1＞0 |
过双曲线
-x2=1的下焦点F作抛物线C：x2=2py（p＞0）的两条切线，切点分别为AB，若FA⊥FB，则抛物线的方程为（ ）
| y2 |
| 3 |
| A、x2=2y |
| B、x2=4y |
| C、x2=6y |
| D、x2=8y |