题目内容
已知sinα=-
,cosα=-
,则角α终边所在的象限是( )
| 1 |
| 2 |
| ||
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:任意角的三角函数的定义
专题:计算题,三角函数的求值
分析:由sinα=-
,cosα=-
,分别确定角α终边所在的象限,即可得出结论.
| 1 |
| 2 |
| ||
| 2 |
解答:
解:∵sinα=-
,∴α终边所在的象限是第三、四象限;
cosα=-
,∴α终边所在的象限是第二、三象限,
∴角α终边所在的象限是第三象限.
故选:C.
| 1 |
| 2 |
cosα=-
| ||
| 2 |
∴角α终边所在的象限是第三象限.
故选:C.
点评:本题考查任意角的三角函数的定义,考查角α终边所在的象限的确定,属于基础题.

练习册系列答案
相关题目
双曲线
-
=1(a>0,b>0),右焦点F2(c,0),A(-a,0),若F2到直线y=
x的距离等于A点到直线y=
x距离的2倍,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| b |
| a |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
双曲线
-y2=1的渐近线方程是( )
| x2 |
| 4 |
| A、y=±2x | ||
| B、y=±4x | ||
C、y=±
| ||
D、y=±
|
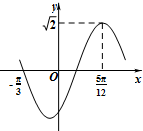
函数f(x)=
sin(ωx+φ)(x∈R,ω>0,|φ|<
)的部分图象如图所示,则ω,φ的值分别是( )
| 2 |
| π |
| 2 |

A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|
“m>0”是“方程
+
=1表示椭圆”的( )
| x2 |
| 2 |
| y2 |
| m |
| A、充分不必要条件 |
| B、充要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
均值都是5的四组数据条形图如下,将四组数据作比较,错误的是( )
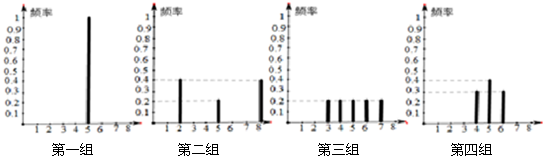

| A、第一组标准差最小 |
| B、第二组极差最大 |
| C、第三组最稳定 |
| D、第三组的方差大于第四组的方差 |