题目内容
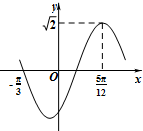
函数f(x)=
sin(ωx+φ)(x∈R,ω>0,|φ|<
)的部分图象如图所示,则ω,φ的值分别是( )
| 2 |
| π |
| 2 |

A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数的图象可得
T,代入周期公式求得ω的值,再由五点作图的第二点列式求得φ的值.
| 3 |
| 4 |
解答:
解:由图知
T=
-(-
)=
π,
∴T=π,即
=π,解得:ω=2.
由五点作图的第二点可知,2×
+φ=
,即φ=-
,满足|φ|<
,
∴ω,φ的值分别是2,-
.
故选:A.
| 3 |
| 4 |
| 5π |
| 12 |
| π |
| 3 |
| 3 |
| 4 |
∴T=π,即
| 2π |
| ω |
由五点作图的第二点可知,2×
| 5π |
| 12 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴ω,φ的值分别是2,-
| π |
| 3 |
故选:A.
点评:本题考查由y=Asin(ωx+φ)的部分图象求解函数解析式,解答的关键是由五点作图的某一点列式求解φ的值,是基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知直线l的方程为2x-2y+b=0(b∈R),则直线l的倾斜角为( )
| A、30° | B、45° |
| C、135° | D、与b有关 |
已知sinα=-
,cosα=-
,则角α终边所在的象限是( )
| 1 |
| 2 |
| ||
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合A={x|
<1},B={x||x|<1},则A∩B=( )
| 1 |
| x |
| A、(-∞,0) | B、(-1,0) |
| C、(0,1) | D、∅ |
f(x)=x+
(x>0)的最小值是( )
| 4 |
| x |
| A、2 | B、1 | C、4 | D、3 |
已知点M(a,b)在直线3x+4y=10上,则
的最小值为( )
| a2+b2 |
| A、2 | ||
| B、3 | ||
C、
| ||
| D、5 |
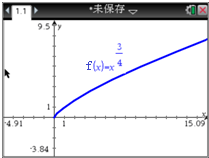 某同学利用TI-Nspire图形计算器作图作出幂函数f(x)=
某同学利用TI-Nspire图形计算器作图作出幂函数f(x)=