题目内容
四边形OABC中，
=
，若
=
，
=
，则
=（ ）
| CB |
| 1 |
| 2 |
| OA |
| OA |
| a |
| OC |
| b |
| AB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：利用向量的多边形法则即可得出．
解答：
解：如图所示，
=
+
+
=-
+
+
=-
+
=-
+
．
故选：D．
| AB |
| AO |
| OC |
| CB |
=-
| OA |
| OC |
| 1 |
| 2 |
| OA |
=-
| 1 |
| 2 |
| OA |
| OC |
=-
| 1 |
| 2 |
| a |
| b |
故选：D．
点评：本题考查了向量的多边形法则，属于基础题．
练习册系列答案
互动英语系列答案
相关题目
当x、y满足条件|x|+|y|＜1时，变量z=
的取值范围是（ ）
| x |
| y-3 |
| A、（-3，3） | ||||
B、（-
| ||||
C、（-∞，-
| ||||
D、（-
|
已知f（x）是定义在[-1，1]上的奇函数，满足f（1）=1，且当a，b∈[-1，1]，a+b≠0，有
＞0．若f（x）≤m2-2am+1（m≠0），对所有的x∈[-1，1]，a∈[-1，1]恒成立，实数m的取值范围是（ ）
| f(a)+f(b) |
| a+b |
| A、（-2，2） |
| B、（-2，0）∪（0，2） |
| C、（-∞，-2]∪[2，+∞） |
| D、（-2，-1）∪（1，2） |
若角α的终边过点（-1，2），则cos2α的值为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知f（x）为奇函数，x＞0时，f（x）=sin2x+cosx，则x＜0时，f（x）为（ ）
| A、sin2x-cosx |
| B、sin2x+cosx |
| C、cosx-sin2x |
| D、-sin2x-cosx |
函数y=-x2+1，-1≤x＜2的值域是（ ）
| A、（-3，0] |
| B、[0，1] |
| C、（-3，1] |
| D、[1，5） |
设集合A={0，a}，B={x∈Z||x|＜2 }，则“a=1”是“A⊆B”的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
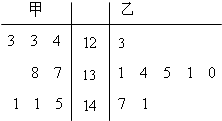为了解某校高一学生的中考数学成绩，分别从甲乙两班随机各抽取8名学生的中考数学成绩，获得如图所示的茎叶图．