题目内容
给出以下四个命题:
①命题“?x<0,x2-x>0”的否定是“?x≥0,x2-x≤0”
②若实数x、y∈[0,1],则满足y>
的概率是
③若随机变量ξ服从正态分布N(2,ξ2)且P(ξ<4)=0.8,则P(0<ξ<2)=0.3
④若a>b≥2,则b2>3b-a
其中真命题有( )
①命题“?x<0,x2-x>0”的否定是“?x≥0,x2-x≤0”
②若实数x、y∈[0,1],则满足y>
| x |
| 2 |
| 3 |
③若随机变量ξ服从正态分布N(2,ξ2)且P(ξ<4)=0.8,则P(0<ξ<2)=0.3
④若a>b≥2,则b2>3b-a
其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接写出全程命题的否定判断①;
利用几何概型结合定积分求概率判断②;
由正态分布的概率公式求概率判断③;
由a>b≥2,作差后根据差式的符号判断④.
利用几何概型结合定积分求概率判断②;
由正态分布的概率公式求概率判断③;
由a>b≥2,作差后根据差式的符号判断④.
解答:
解:对于①,命题“?x<0,x2-x>0”的否定是“?x<0,x2-x≤0”
∴命题①是假命题;
对于②,由y>
,得y2>x,
如图,
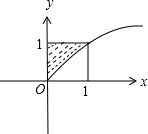
满足y>
的概率是
=
=
.
∴命题②是假命题;
对于③,随机变量ξ服从正态分布N(2,ξ2)且P(ξ<4)=0.8,
则P(0<ξ<2)=0.5-P(ξ>4)=0.3.
∴命题③是真命题;
对于④,∵a>b≥2,
∴b2 -3b+a=(a-b)+b(b-2)>0+0=0.
∴命题④是真命题.
∴真命题的个数是2.
故选:B.
∴命题①是假命题;
对于②,由y>
| x |
如图,

满足y>
| x |
1
| ||||
| 1 |
1-
| ||||||
| 1 |
| 1 |
| 3 |
∴命题②是假命题;
对于③,随机变量ξ服从正态分布N(2,ξ2)且P(ξ<4)=0.8,
则P(0<ξ<2)=0.5-P(ξ>4)=0.3.
∴命题③是真命题;
对于④,∵a>b≥2,
∴b2 -3b+a=(a-b)+b(b-2)>0+0=0.
∴命题④是真命题.
∴真命题的个数是2.
故选:B.
点评:本题考查命题的真假判断与应用,考查了几何概型概率的求法,训练了作差法比较两个代数式的大小,是中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
当x、y满足条件|x|+|y|<1时,变量z=
的取值范围是( )
| x |
| y-3 |
| A、(-3,3) | ||||
B、(-
| ||||
C、(-∞,-
| ||||
D、(-
|
函数y=-x2+1,-1≤x<2的值域是( )
| A、(-3,0] |
| B、[0,1] |
| C、(-3,1] |
| D、[1,5) |
设集合A={0,a},B={x∈Z||x|<2 },则“a=1”是“A⊆B”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
已知集合A={2a},B={a,b),若A∩B={
},则A∪B为( )
| 1 |
| 2 |
A、{
| ||
B、{-1,
| ||
C、{
| ||
D、{-1,
|
已知θ为实数,若复数z=sin2θ-1+i(
cosθ-1)是纯虚数,则z的虚部为( )
| 2 |
| A、2 | B、0 | C、-2 | D、-2i |
已知命题p:若非零实数a,b,则
<
;命题q:对任意实数x∈(0,+∞),log
(x+1)<0,则下列命题为真命题的是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| A、p且q | B、p或¬q |
| C、¬p且q | D、p且¬q |
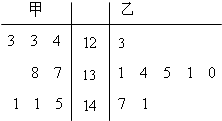 为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.
为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.