题目内容
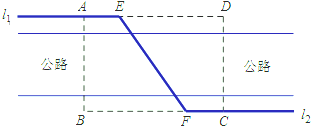
二次函数y=f（x）的图象的一部分如图所示（1）根据图象写出f（x）在区间[-1，4]上的值域；
（2）根据图象求y=f（x）的解析式；
（3）当k∈R时，试探讨关于x的方程f（x）-k=0在（-1，4]上的解的个数．
考点：二次函数的性质
专题：函数的性质及应用
分析：（1）由图象直接读出即可，（2）将函数的解析式设为两根式，代入交点求出即可；（3）结合图象将k分区间进行讨论．
解答：
解：（1）由图象得：f（x）在区间[-1，4]上的值域为：[-4，5]．
（2）由图象得：f（x）在x轴上的交点为：（-1，0），（3，0），
∴设解析式为：y=a（x+1）（x-3）①，
又∵顶点坐标为：（-4，1），
把顶点代入①得：a=1，
∴f（x）=x2-2x-3．
（3）①当k＞5时，关于x的方程f（x）-k=0在（-1，4]上无解，
②当0＜k≤5时，关于x的方程f（x）-k=0在（-1，4]上有一个解．
③当-4＜k≤0时，关于x的方程f（x）-k=0在（-1，4]上的解有2个．
④k=-4时，关于x的方程f（x）-k=0在（-1，4]上的解有1个．
⑤k＜-4时，关于x的方程f（x）-k=0在（-1，4]上无解．
（2）由图象得：f（x）在x轴上的交点为：（-1，0），（3，0），
∴设解析式为：y=a（x+1）（x-3）①，
又∵顶点坐标为：（-4，1），
把顶点代入①得：a=1，
∴f（x）=x2-2x-3．
（3）①当k＞5时，关于x的方程f（x）-k=0在（-1，4]上无解，
②当0＜k≤5时，关于x的方程f（x）-k=0在（-1，4]上有一个解．
③当-4＜k≤0时，关于x的方程f（x）-k=0在（-1，4]上的解有2个．
④k=-4时，关于x的方程f（x）-k=0在（-1，4]上的解有1个．
⑤k＜-4时，关于x的方程f（x）-k=0在（-1，4]上无解．
点评：本题考查了函数的性质问题，解题时注意结合图象，本题渗透了分类讨论思想，属于中档题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
函数y=-x2+1，-1≤x＜2的值域是（ ）
| A、（-3，0] |
| B、[0，1] |
| C、（-3，1] |
| D、[1，5） |
已知命题p：若非零实数a，b，则
＜
；命题q：对任意实数x∈（0，+∞），log
（x+1）＜0，则下列命题为真命题的是（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| A、p且q | B、p或￢q |
| C、￢p且q | D、p且￢q |
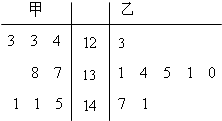为了解某校高一学生的中考数学成绩，分别从甲乙两班随机各抽取8名学生的中考数学成绩，获得如图所示的茎叶图．
