题目内容
已知数列{an}的前n项和为Sn,数列{bn}满足bn=log2(an+1),a1=1且对于任意n≥2,n∈N+有an=2an-1+1.
(1)证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(2)若cn=an•bn,求数列{cn}的前n项和Tn.
(1)证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(2)若cn=an•bn,求数列{cn}的前n项和Tn.
考点:等差数列与等比数列的综合,数列的求和
专题:等差数列与等比数列
分析:(1)通过已知条件,利用等比数列的定义,直接求出an+1=2(an-1+1),即可求证数列{an+1}是等比数列;
(2)利用(1)直接求数列{an}的通项公式an,然后求出{bn}的通项公式bn,可得cn=an•bn的通项公式,利用分组求和法和错位相减法,可得答案.
(2)利用(1)直接求数列{an}的通项公式an,然后求出{bn}的通项公式bn,可得cn=an•bn的通项公式,利用分组求和法和错位相减法,可得答案.
解答:
证明:(1)当n=1时,S1=2a1-1,得a1=1. (1分)
∵Sn=2an-n,
∴当n≥2时,Sn-1=2an-1-(n-1),
两式相减得:an=2an-2an-1-1,
∴an=2an-1+1. (3分)
∴an+1=2an-1+2=2(an-1+1),(5分)
∴{an+1}是以a1+1=2为首项,2为公比的等比数列. (6分)
解:(2)∵(2)由(1)得an+1=2•2n-1=2n,∴an=2n-1,n∈N*. (8分)
∴bn=log2(an+1)=log22n=n,n∈N*. (10分)
cn=an•bn=n(2n-1)=n•2n-n,
令T′=1×2+2×22+3×23+…+(n-1)×2n-1+n×2n,…①,
2T′=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1,…②
①-②得:
-T'=2+22+23+…+2n-1+2n-n×2n+1=-2(1-2n)-n•2n+1T'=2+(n-1)•2n+1…(10分)
故T″=1+2+3+…+n=
…(11分)
T=T′-T″=2+(n-1)•2n+1-
.…(12分)
∵Sn=2an-n,
∴当n≥2时,Sn-1=2an-1-(n-1),
两式相减得:an=2an-2an-1-1,
∴an=2an-1+1. (3分)
∴an+1=2an-1+2=2(an-1+1),(5分)
∴{an+1}是以a1+1=2为首项,2为公比的等比数列. (6分)
解:(2)∵(2)由(1)得an+1=2•2n-1=2n,∴an=2n-1,n∈N*. (8分)
∴bn=log2(an+1)=log22n=n,n∈N*. (10分)
cn=an•bn=n(2n-1)=n•2n-n,
令T′=1×2+2×22+3×23+…+(n-1)×2n-1+n×2n,…①,
2T′=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1,…②
①-②得:
-T'=2+22+23+…+2n-1+2n-n×2n+1=-2(1-2n)-n•2n+1T'=2+(n-1)•2n+1…(10分)
故T″=1+2+3+…+n=
| (1+n)n |
| 2 |
T=T′-T″=2+(n-1)•2n+1-
| n(1+n) |
| 2 |
点评:本题是综合题,考查数列的基本性质,等比数列的证明,通项公式的求法,数列求和,考查计算能力,注意解题方法的应用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
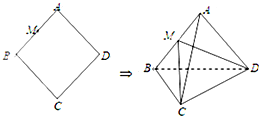 在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为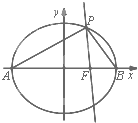 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为