题目内容
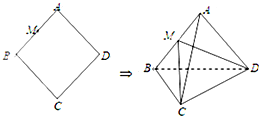 在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为| 9 |
| 25 |
(1)求证:平面ABD⊥平面CBD;
(2)若M是AB的中点,求三棱锥A-MCD的体积.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出AO⊥平面BCD,由此能证明平面ABD⊥平面CBD.
(Ⅱ)分别以OA,OC,OD所在直线为坐标轴建系,利用向量法能求出三棱锥A-MCD的体积.
(Ⅱ)分别以OA,OC,OD所在直线为坐标轴建系,利用向量法能求出三棱锥A-MCD的体积.
解答:
(Ⅰ)证明:菱形ABCD中,记AC,BD交点为O,AD=5,∴OA=4,OD=3,
翻折后变成三棱椎A-BCD,在△ACD中,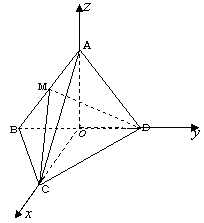
AC2=AD2+CD2-2AD•CD•cos∠ADC
=25+25-2×5×5×
,
在△AOC中,OA2+OC2=32=AC2,
∴∠AOC=90°,即AO⊥OC,又AO⊥BD,OC∩BD=O,
∴AO⊥平面BCD,
又AO?平面ABD,∴平面ABD⊥平面CBD.
(Ⅱ)解:由(Ⅰ)知OA,OC,OD两两互相垂直,分别以OA,OC,OD所在直线为坐标轴建系,
则A (0,0,4),B(0,-3,0),C(4,0,0),D(0,3,0),M(0,-
,2),
=(4,
,-2),
=(4,0,-4),
=(4,-3,0),
设平面ACD的一个法向量
=(x,y,z),
则由
,得
,
令y=4,得
=(3,4,3),
∵
=(0,
,2),∴A到平面ACD的距离d=
=
=
.
∵在边长为5的菱形ABCD中,AC=8,
∴S△ACD=
×2
×4=12,
∴三棱锥A-MCD的体积V=
×S△ACD×d=
×12×
=
.
翻折后变成三棱椎A-BCD,在△ACD中,

AC2=AD2+CD2-2AD•CD•cos∠ADC
=25+25-2×5×5×
| 9 |
| 25 |
在△AOC中,OA2+OC2=32=AC2,
∴∠AOC=90°,即AO⊥OC,又AO⊥BD,OC∩BD=O,
∴AO⊥平面BCD,
又AO?平面ABD,∴平面ABD⊥平面CBD.
(Ⅱ)解:由(Ⅰ)知OA,OC,OD两两互相垂直,分别以OA,OC,OD所在直线为坐标轴建系,
则A (0,0,4),B(0,-3,0),C(4,0,0),D(0,3,0),M(0,-
| 3 |
| 2 |
| MC |
| 3 |
| 2 |
| AC |
| DC |
设平面ACD的一个法向量
| n |
则由
|
|
令y=4,得
| n |
∵
| MA |
| 3 |
| 2 |
|
| ||||
|
|
| |0+6+6| | ||
|
6
| ||
| 17 |
∵在边长为5的菱形ABCD中,AC=8,
∴S△ACD=
| 1 |
| 2 |
| 25-16 |
∴三棱锥A-MCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
6
| ||
| 17 |
24
| ||
| 17 |
点评:本题考查平面与平面垂直的证明,考查三棱锥的体积的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知圆锥的表面积为9πcm2,且它的侧面展开图是一个半圆,则圆锥的底面半径为( )
A、
| ||||
B、3
| ||||
C、
| ||||
D、2
|
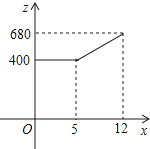 我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表:
我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表: