题目内容
已知椭圆Q的中心为坐标原点,焦点在x轴上,离心率e=
,过椭圆Q右焦点且垂直于x轴的一条直线交椭圆于E,F两点,|EF|=1.
(Ⅰ)求椭圆Q的方程;
(Ⅱ)已知两点C(-
,0),D(
,0),设A,B,M是椭圆Q上的三点,满足
=
+
,点N为线段AB的中点,求|NC|+|ND|的值.
| ||
| 2 |
(Ⅰ)求椭圆Q的方程;
(Ⅱ)已知两点C(-
| ||
| 2 |
| ||
| 2 |
| OM |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
考点:直线与圆锥曲线的综合问题
专题:向量与圆锥曲线
分析:(Ⅰ)由题意设出椭圆方程,结合已知列出关于a,b,c的方程组,求出a,b后可得椭圆的方程;
(Ⅱ)设出A,B的坐标,由
=
+
得到M的坐标,把M的坐标代入椭圆方程得到
有
•(
x1+
x2)2+(
y1+
y2)2=1,再由A,B在椭圆上整理可得点N在椭圆
+2y2=1上,且C,D为该椭圆的两个焦点坐标,则答案可求.
(Ⅱ)设出A,B的坐标,由
| OM |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
有
| 1 |
| 4 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| x2 |
| 2 |
解答:
解:(Ⅰ) 依据题意可设椭圆Q:
+
=1(a>b>0),F(c,0),则有:
,解得
,
∴椭圆Q:
+y2=1;
(Ⅱ)设A(x1,y1),B(x2,y2),则
+
=1,
+
=1 ①,
由
=
+
,得M(
x1+
x2,
y1+
y2),
又点M在椭圆Q:
+y2=1上,
则有
•(
x1+
x2)2+(
y1+
y2)2=1 ②,
综合①、②得:
+y1•y2=0.
又线段AB的中点为N(
,
),
且
(
)2+(
)2
=
(
+y12)+
(
+y12)+
(
+y1•y2)
=
+
=
.
上式表明,点N在椭圆
+2y2=1上,且该椭圆的两个焦点恰好为C(-
,0),D(
,0)两点,
由椭圆定义有|NC|+|ND|=2
.
| x2 |
| a2 |
| y2 |
| b2 |
|
|
∴椭圆Q:
| x2 |
| 4 |
(Ⅱ)设A(x1,y1),B(x2,y2),则
| ||
| 4 |
| y | 2 1 |
| ||
| 4 |
| y | 2 2 |
由
| OM |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
又点M在椭圆Q:
| x2 |
| 4 |
则有
| 1 |
| 4 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
综合①、②得:
| x1•x2 |
| 4 |
又线段AB的中点为N(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
且
| 1 |
| 4 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
=
| 1 |
| 4 |
| x12 |
| 4 |
| 1 |
| 4 |
| x12 |
| 4 |
| 1 |
| 2 |
| x1•x2 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
上式表明,点N在椭圆
| x2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
由椭圆定义有|NC|+|ND|=2
| 2 |
点评:本题考查了椭圆方程的求法,主要考查了直线与椭圆的位置关系的应用,训练了“舍而不求”的数学解题思想方法,圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是压轴题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
已知集合A={x|y=lnx},集合B={x∈Z||x|≤2},则A∩B=( )
| A、(1,2) |
| B、{1,2} |
| C、(0,2) |
| D、{0,1,2} |
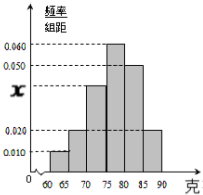 某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个.
某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个. 如图,四棱锥P-ABCD中,△PAB是正三角形,四边形ABCD是矩形,且平面PAB⊥平面ABCD,PA=2,PC=4.
如图,四棱锥P-ABCD中,△PAB是正三角形,四边形ABCD是矩形,且平面PAB⊥平面ABCD,PA=2,PC=4.