题目内容
已知椭圆C:
+
=1(a>b>0)的左、右焦点F1,F2,M是椭圆上任意一点,若以坐标原点为圆心,椭圆短轴长为直径的圆恰好经过椭圆的焦点,且△MF1F2的周长为4+2
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l是圆O:x2+y2=
上动点P(x0,y0)(x0•y0≠0)处的切线,l与椭圆C交与不同的两点Q,R,证明:∠QOR的大小为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l是圆O:x2+y2=
| 4 |
| 3 |
考点:直线与圆锥曲线的关系,圆的切线方程,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据以坐标原点为圆心,椭圆短轴长为直径的圆经过椭圆的焦点,可得b=c,利用△PF1F2的周长为4+2
,可得a+c=2+
,从而可求椭圆的几何量,进而可得椭圆C的方程;
(Ⅱ)设直线的l方程与椭圆方程联立,记Q(x1,y1),R(x2,y2),利用韦达定理,确定x1x2+y1y2=0,即可证得结论.
| 2 |
| 2 |
(Ⅱ)设直线的l方程与椭圆方程联立,记Q(x1,y1),R(x2,y2),利用韦达定理,确定x1x2+y1y2=0,即可证得结论.
解答:
(Ⅰ)解:因为以坐标原点为圆心,椭圆短轴长为直径的圆经过椭圆的焦点,所以b=c,可得a=
c,
又因为△PF1F2的周长为4+2
,所以a+c=2+
,所以c=
,
所以a=2,b=
,所以所求椭圆C的方程为
+
=1. …(5分)
(Ⅱ)证明:直线的l方程为x0x+y0y=
,且x02+y02=
,记Q(x1,y1),R(x2,y2),
联立直线与椭圆方程,消去y得(2x02+y02)x2-
x0x+
-4y02=0,
∴x1+x2=
,x1x2=
,…(8分)
∴y1y2=
,…(10分)
∴x1x2+y1y2=
+
=0
∴∠QOR=90°为定值.…(12分)
| 2 |
又因为△PF1F2的周长为4+2
| 2 |
| 2 |
| 2 |
所以a=2,b=
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
(Ⅱ)证明:直线的l方程为x0x+y0y=
| 4 |
| 3 |
| 4 |
| 3 |
联立直线与椭圆方程,消去y得(2x02+y02)x2-
| 16 |
| 3 |
| 32 |
| 9 |
∴x1+x2=
| ||
| 2x02+y02 |
| ||
| 2x02+y02 |
∴y1y2=
| ||
| 2x02+y02 |
∴x1x2+y1y2=
| ||
| 2x02+y02 |
| ||
| 2x02+y02 |
∴∠QOR=90°为定值.…(12分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
相关题目
已知集合A={x|y=lnx},集合B={x∈Z||x|≤2},则A∩B=( )
| A、(1,2) |
| B、{1,2} |
| C、(0,2) |
| D、{0,1,2} |
 若函数f(x)=
若函数f(x)=| 1 |
| 2 |
| A、λ1<λ2 |
| B、λ1>λ2 |
| C、|λ1|<|λ2| |
| D、|λ1|>|λ2| |
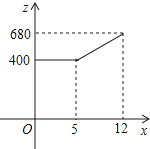 我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表:
我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表: 如图,四棱锥P-ABCD中,△PAB是正三角形,四边形ABCD是矩形,且平面PAB⊥平面ABCD,PA=2,PC=4.
如图,四棱锥P-ABCD中,△PAB是正三角形,四边形ABCD是矩形,且平面PAB⊥平面ABCD,PA=2,PC=4.