题目内容
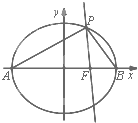 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为2
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为2| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线AP与直线x=2交于点D.试判断以BD为直径的圆与直线PF的位置关系,并证明你的结论.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设椭圆C方程,利用右焦点为F(1,0),△APB面积的最大值为2
,建立方程组,即可求椭圆C的方程;
(Ⅱ)设直线AP的方程,可得D的坐标,直线方程代入椭圆方程,利用韦达定理求出P的坐标,分类讨论,结合点到直线的距离公式,即可得出结论.
| 3 |
(Ⅱ)设直线AP的方程,可得D的坐标,直线方程代入椭圆方程,利用韦达定理求出P的坐标,分类讨论,结合点到直线的距离公式,即可得出结论.
解答:
(Ⅰ)解:由题意可设椭圆C方程为:
+
=1(a>b>0),则
因为右焦点为F(1,0),△APB面积的最大值为2
,
所以
,
所以a=2,b=
,
所以椭圆C的方程为
+
=1.
(Ⅱ)以BD为直径的圆与直线PF相切.
证明:由题意,设直线AP的方程为y=k(x+2)(k≠0).
则点D坐标为(2,4k),BD中点E的坐标为(2,2k).
由直线方程代入椭圆方程可得(3+4k2)x2+16k2x+16k2-12=0.
设点P的坐标为(x0,y0),则-2x0=
.
所以x0=
,y0=
.
因为点F坐标为(1,0),
当k=±
时,点P的坐标为(1,±
),点D的坐标为(2,±2).
直线PF⊥x轴,此时以BD为直径的圆(x-2)2+(y-2k)2=1与直线PF相切.
当k≠±
时,则直线PF的斜率
=
.
所以直线PF的方程为y=
(x-1).
点E到直线PF的距离d=
=2|k|.
又因为|BD|=4|k|,所以d=
|BD|.
故以BD为直径的圆与直线PF相切.
综上得,以BD为直径的圆与直线PF相切.
| x2 |
| a2 |
| y2 |
| b2 |
因为右焦点为F(1,0),△APB面积的最大值为2
| 3 |
所以
|
所以a=2,b=
| 3 |
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)以BD为直径的圆与直线PF相切.
证明:由题意,设直线AP的方程为y=k(x+2)(k≠0).
则点D坐标为(2,4k),BD中点E的坐标为(2,2k).
由直线方程代入椭圆方程可得(3+4k2)x2+16k2x+16k2-12=0.
设点P的坐标为(x0,y0),则-2x0=
| 16k2-12 |
| 3+4k2 |
所以x0=
| 6-8k2 |
| 3+4k2 |
| 12k |
| 3+4k2 |
因为点F坐标为(1,0),
当k=±
| 1 |
| 2 |
| 3 |
| 2 |
直线PF⊥x轴,此时以BD为直径的圆(x-2)2+(y-2k)2=1与直线PF相切.
当k≠±
| 1 |
| 2 |
| y0 |
| x0-1 |
| 4k |
| 1-4k2 |
所以直线PF的方程为y=
| 4k |
| 1-4k2 |
点E到直线PF的距离d=
|
| ||||
|
又因为|BD|=4|k|,所以d=
| 1 |
| 2 |
故以BD为直径的圆与直线PF相切.
综上得,以BD为直径的圆与直线PF相切.
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
若复数z与(z-1)2-2i都是纯虚数,则z=( )
| A、i | B、-i | C、±i | D、1 |
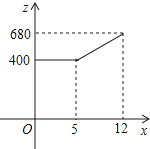 我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表:
我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表: