题目内容
已知函数f(x)=x3-ax2-2在(2,+∞)上是增函数,则a的取值范围是 .
考点:利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:先对函数f(x)=x3-ax2-2进行求导,转化成f′(x)在(2,+∞)上恒有f′(x)≥0问题,进而求出参数a的取值范围.
解答:
解:函数f(x)=x3-ax2-2的导数为f′(x)=3x2-2ax,
∵f(x)在(2,+∞)上是增函数,
∴f′(x)在(2,+∞)上恒有f′(x)≥0,
即3x2-2ax≥0即有2a≤3x在(2,+∞)上恒成立.
则必有2a≤6,则a≤3.
实数a的取值范围是(-∞,3].
故答案为:(-∞,3].
∵f(x)在(2,+∞)上是增函数,
∴f′(x)在(2,+∞)上恒有f′(x)≥0,
即3x2-2ax≥0即有2a≤3x在(2,+∞)上恒成立.
则必有2a≤6,则a≤3.
实数a的取值范围是(-∞,3].
故答案为:(-∞,3].
点评:本题主要考查函数单调性的综合运用,函数的单调性特征与导数之间的综合应用能力,把两个知识加以有机组合.

练习册系列答案
相关题目
若椭圆的中心在原点,一个焦点为(0,2),直线y=3x+7与椭圆相交所得弦的中点的纵坐标为1,则这个椭圆的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
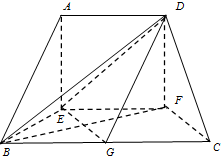 已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF=
已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF= 在正方体ABCD-A1B1C1D1中,E,F分别为DD1,BD的中点.求证:
在正方体ABCD-A1B1C1D1中,E,F分别为DD1,BD的中点.求证: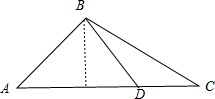 如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.
如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.