题目内容
一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（ ）| A、1 | B、2 | C、3 | D、4 |
考点：球内接多面体,由三视图求面积、体积,球的体积和表面积
专题：计算题,空间位置关系与距离
分析：由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r．
解答：
解：由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r，则
8-r+6-r=
，
∴r=2．
故选：B．
8-r+6-r=
| 82+62 |
∴r=2．
故选：B．
点评：本题考查三视图，考查几何体的内切圆，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
阅读如图程序框图，运行相应的程序，则程序运行后输出的结果为（ ）
| A、7 | B、9 | C、10 | D、11 |
已知抛物线C：y2=x的焦点为F，A（x0，y0）是C上一点，|AF|=
x0，x0=（ ）
| 5 |
| 4 |
| A、1 | B、2 | C、4 | D、8 |
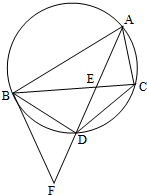如图，△ABC是圆的内接三角形，∠BAC的平分线交圆于点D，交BC于E，过点B的圆的切线与AD的延长线交于点F，在上述条件下，给出下列四个结论：①BD平分∠CBF；
②FB2=FD•FA；
③AE•CE=BE•DE；
④AF•BD=AB•BF．
所有正确结论的序号是（ ）
| A、①② | B、③④ |
| C、①②③ | D、①②④ |
已知集合M={2，4}，N={1，2}，P={x|x=
，a∈M，b∈N}，则集合P的子集个数为（ ）
| a |
| b |
| A、3 | B、4 | C、8 | D、16 |