题目内容
已知数列{an}的前n项和为Sn,且满足Sn=
n2+
n.数列{bn}满足b1=1,2bn-bn-1=0(n≥2,n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求数列{an}和{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
考点:数列的求和,数列的概念及简单表示法
专题:等差数列与等比数列
分析:(1)利用公式法求得an利用等比数列的定义求得bn;
(2)利用错位相减法求得数列的和即可.
(2)利用错位相减法求得数列的和即可.
解答:
解:(Ⅰ)当n>1时,an=Sn-Sn-1=n,
当n=1时,求得a1=s1=1.所以an=n.
因为
=
且b1=1,所以bn=(
)n-1.…(6分)
(Ⅱ)由(Ⅰ),知cn=n•(
)n-1.
所以Tn=1•(
)0+2•(
)1+…+n•(
)n-1,
Tn=1•(
)1+2•(
)2+…+n•(
)n,
于是
Tn=1+(
)1+(
)2+…+(
)n-1-n•(
)n=
-n•(
)n,
化简,得Tn=4-
.…(12分)
当n=1时,求得a1=s1=1.所以an=n.
因为
| bn |
| bn-1 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ),知cn=n•(
| 1 |
| 2 |
所以Tn=1•(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
于是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
1-(
| ||
1-
|
| 1 |
| 2 |
化简,得Tn=4-
| 2n+4 |
| 2n |
点评:本题主要考查公式法求数列的通项公式及等比数列的定义,考查数列求和的方法错位相减法,考查学生的运算能力,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)=( )
| A、45 | B、60 |
| C、120 | D、210 |
 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )| A、1 | B、2 | C、3 | D、4 |
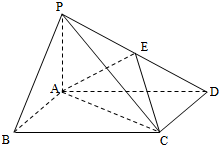 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE.
如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE. 如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=
如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=