题目内容
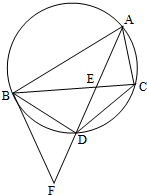如图，△ABC是圆的内接三角形，∠BAC的平分线交圆于点D，交BC于E，过点B的圆的切线与AD的延长线交于点F，在上述条件下，给出下列四个结论：①BD平分∠CBF；
②FB2=FD•FA；
③AE•CE=BE•DE；
④AF•BD=AB•BF．
所有正确结论的序号是（ ）
| A、①② | B、③④ |
| C、①②③ | D、①②④ |
考点：与圆有关的比例线段,命题的真假判断与应用
专题：直线与圆
分析：本题利用角与弧的关系，得到角相等，再利用角相等推导出三角形相似，得到边成比例，即可选出本题的选项．
解答：
解：∵圆周角∠DBC对应劣弧CD，圆周角∠DAC对应劣弧CD，
∴∠DBC=∠DAC．
∵弦切角∠FBD对应劣弧BD，圆周角∠BAD对应劣弧BD，
∴∠FBD=∠BAF．
∵AD是∠BAC的平分线，
∴∠BAF=∠DAC．
∴∠DBC=∠FBD．即BD平分∠CBF．即结论①正确．
又由∠FBD=∠FAB，∠BFD=∠AFB，得△FBD～△FAB．
由
=
，FB2=FD•FA．即结论②成立．
由
=
，得AF•BD=AB•BF．即结论④成立．
正确结论有①②④．
故答案为D
∴∠DBC=∠DAC．
∵弦切角∠FBD对应劣弧BD，圆周角∠BAD对应劣弧BD，
∴∠FBD=∠BAF．
∵AD是∠BAC的平分线，
∴∠BAF=∠DAC．
∴∠DBC=∠FBD．即BD平分∠CBF．即结论①正确．
又由∠FBD=∠FAB，∠BFD=∠AFB，得△FBD～△FAB．
由
| FB |
| FA |
| FD |
| FB |
由
| BF |
| AF |
| BD |
| AB |
正确结论有①②④．
故答案为D
点评：本题考查了弦切角、圆周角与弧的关系，还考查了三角形相似的知识，本题总体难度不大，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
掷两颗均匀的骰子，则点数之和为5的概率等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（ ）| A、1 | B、2 | C、3 | D、4 |
设z=
+i，则|z|=（ ）
| 1 |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
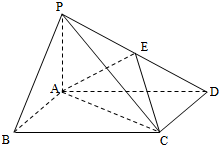如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．