题目内容
△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cosA=
,B=A+
.
(Ⅰ)求b的值;
(Ⅱ)求△ABC的面积.
| ||
| 3 |
| π |
| 2 |
(Ⅰ)求b的值;
(Ⅱ)求△ABC的面积.
考点:正弦定理
专题:解三角形
分析:(Ⅰ)利用cosA求得sinA,进而利用A和B的关系求得sinB,最后利用正弦定理求得b的值.
(Ⅱ)利用sinB,求得cosB的值,进而根两角和公式求得sinC的值,最后利用三角形面积公式求得答案.
(Ⅱ)利用sinB,求得cosB的值,进而根两角和公式求得sinC的值,最后利用三角形面积公式求得答案.
解答:
解:(Ⅰ)∵cosA=
,
∴sinA=
=
,
∵B=A+
.
∴sinB=sin(A+
)=cosA=
,
由正弦定理知
=
,
∴b=
•sinB=
×
=3
.
(Ⅱ)∵sinB=
,B=A+
>
∴cosB=-
=-
,
sinC=sin(π-A-B)=sin(A+B)=sinAcosB+cosAsinB=
×(-
)+
×
=
,
∴S=
a•b•sinC=
×3×3
×
=
.
| ||
| 3 |
∴sinA=
1-
|
| ||
| 3 |
∵B=A+
| π |
| 2 |
∴sinB=sin(A+
| π |
| 2 |
| ||
| 3 |
由正弦定理知
| a |
| sinA |
| b |
| sinB |
∴b=
| a |
| sinA |
| 3 | ||||
|
| ||
| 3 |
| 2 |
(Ⅱ)∵sinB=
| ||
| 3 |
| π |
| 2 |
| π |
| 2 |
∴cosB=-
1-
|
| ||
| 3 |
sinC=sin(π-A-B)=sin(A+B)=sinAcosB+cosAsinB=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
3
| ||
| 2 |
点评:本题主要考查了正弦定理的应用.解题过程中结合了同角三角函数关系,三角函数恒等变换的应用,注重了基础知识的综合运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了得到函数y=sin3x+cos3x的图象,可以将函数y=
cos3x的图象( )
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
掷两颗均匀的骰子,则点数之和为5的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )| A、1 | B、2 | C、3 | D、4 |
设z=
+i,则|z|=( )
| 1 |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
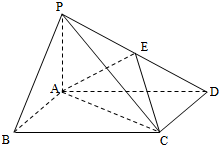 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.