题目内容
19.某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)项目 类别 | 年固定 成本 | 每件产品 成本 | 每件产品 销售价 | 每年最多可 生产的件数 |
| A产品 | 20 | m | 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其定义域;
(2)如何投资最合理(可获得最大年利润)?请你做出规划.
分析 (1)利用“利润=收入-成本”分别代入计算即得结论;
(2)通过(1)分别计算出两种产品的年利润最大值,进而作差比较即得结论.
解答 解:(1)由年销售量为x件,按利润的计算公式,有生产A、B两产品的年利润y1,y2分别为:
y1=10x-(20+cx)=(10-c)x-20(0≤x≤200且x∈N),
y2=18x-(40+8x)-0.05x2=-0.05(x-100)2+460(0≤x≤120且x∈N),
(2)∵6≤c≤9,
∴10-c>0,
∴y1=(10-c)x-20为增函数,
又∵0≤x≤200,x∈N,
∴当x=200时,生产A产品有最大利润为(10-c)×200-20=1980-200c(万美元),
又∵y2=-0.05(x-100)2+460(0≤x≤120且x∈N),
∴当x=100时,生产B产品有最大利润为460,
因为(y1)max-(y2)max=(1980-200c)-460=1520-200c=$\left\{\begin{array}{l}{>0,}&{6≤c<7.6}\\{=0,}&{c=7.6}\\{<0,}&{7.6<c≤9}\end{array}\right.$,
所以,当6≤c<7.6时,可投资生产A产品200件;
当c=7.6时,生产A产品与生产B产品均可;
当7.6<c≤9时,可投资生产B产品100件.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
4.若无穷等差数列{an}的首项a1>0,公差d<0,{an}的前n项和为Sn,则( )
| A. | Sn单调递减 | B. | Sn单调递增 | C. | Sn有最大值 | D. | Sn有最小值 |
11.函数f(x)=log4x与g(x)=22x的图象( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
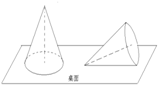 用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.