题目内容
4．若无穷等差数列{an}的首项a1＞0，公差d＜0，{an}的前n项和为Sn，则（ ）| A． | Sn单调递减 | B． | Sn单调递增 | C． | Sn有最大值 | D． | Sn有最小值 |
分析 化简可得{an}是递减数列，且先正值，后负值；从而判断出Sn有最大值．
解答 解：∵无穷等差数列{an}的首项a1＞0，公差d＜0，
∴{an}是递减数列，且先正值，后负值；
∴{an}的前n项和为Sn先增加，后减小；
∴Sn有最大值；
故选C．
点评 本题考查了单调性数列的应用及前n项和的最值的判断．
练习册系列答案
相关题目
15．含有甲、乙、丙的六位同学站成一排，则甲、乙相邻且甲、丙两人中间恰有两人的站法的种数为（ ）
| A． | 72 | B． | 60 | C． | 32 | D． | 24 |
19．某企业为打入国际市场，决定从A、B两种产品中只选择一种进行投资生产．已知投资生产这两种产品的有关数据如下表：（单位：万美元）
其中年固定成本与年生产的件数无关，c为待定常数，其值由生产A产品的原材料价格决定，预计c∈[6，9]另外，年销售x件B产品时需上交0.05x2万美元的特别关税．假设生产出来的产品都能在当年销售出去．
（1）写出该厂分别投资生产A、B两种产品的年利润y1，y2与生产相应产品的件数x之间的函数关系并指明其定义域；
（2）如何投资最合理（可获得最大年利润）？请你做出规划．
项目 类别 | 年固定 成本 | 每件产品 成本 | 每件产品 销售价 | 每年最多可 生产的件数 |
| A产品 | 20 | m | 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
（1）写出该厂分别投资生产A、B两种产品的年利润y1，y2与生产相应产品的件数x之间的函数关系并指明其定义域；
（2）如何投资最合理（可获得最大年利润）？请你做出规划．
函数f（x）与g（x）的图象拼成如图所示的“Z”字形折线段ABOCD，不含A（0，1），B（1，1），O（0，0），C（-1，-1），D（0，-1）五个点，若f（x）的图象关于原点对称的图形即为g（x）的图象，则其中一个函数的解析式可以为f（x）=$\left\{\begin{array}{l}{x，-1＜x＜0}\\{1，0＜x＜1}\end{array}\right.$．
13．函数$y={3^{{x^2}-1}}（-1≤x＜0）$的反函数是（ ）
| A． | $y=-\sqrt{1+{{log}_3}x}（x≥\frac{1}{3}）$ | B． | $y=-\sqrt{1+{{log}_3}x}（\frac{1}{3}＜x≤1）$ | ||
| C． | $y=\sqrt{1+{{log}_3}x}（\frac{1}{3}＜x≤1）$ | D． | $y=\sqrt{1+{{log}_3}x}（x≥\frac{1}{3}）$ |
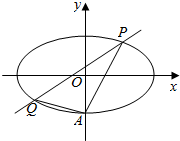如图，椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点A（0，-1），且离心率为$\frac{\sqrt{2}}{2}$．