题目内容
2.已知函数$f(x)=2{sin^2}x+\sqrt{3}sin2x+1$.求:(1)f(x)的单调递增区间;
(2)f(x)在$[0,\frac{π}{2}]$上的最值.
分析 (1)先根据两角和公式对函数解析式进行化简,再根据正弦函数的性质得出答案.
(2)确定变量的范围,即可求出f(x)在$[0,\frac{π}{2}]$上的最值.
解答 解:(1)$f(x)=2{sin^2}x+\sqrt{3}sin2x+1$=$1-cos2x+\sqrt{3}sin2x+1$
=$\sqrt{3}sin2x-cos2x+2$
=$2sin(2x-\frac{π}{6})+2$
$\begin{array}{l}∴-\frac{π}{2}+2kπ≤2x-\frac{π}{6}≤\frac{π}{2}+2kπ\\∴-\frac{π}{6}+kπ≤x≤\frac{π}{3}+kπ\end{array}$
∴f(x)的单调递增区间为$[{-\frac{π}{6}+kπ,\frac{π}{3}+kπ}]$
(2)∵$0≤x≤\frac{π}{2}$
∴$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{5π}{6}$
∴$sin(2x-\frac{π}{6})∈[{-\frac{1}{2},1}]$
∴f(x)∈[1,4].
点评 本题主要考查两角和公式及三角函数单调性、最值问题.把三角函数化简成y=Asin(ωx+φ)的形式很关键.

练习册系列答案
相关题目
7.若直线3x-4y+5=0与圆x2+y2=r2(r>0)相交于A,B两点且∠AOB=120°则r=( )
| A. | 1 | B. | 2 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
14.“a>0,b>0”是“$ab<{({\frac{a+b}{2}})^2}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=4b,若这样的直线有且仅有两条,则离心率e的取值范围是( )
| A. | $({1,\frac{{\sqrt{5}}}{2}})$ | B. | $({\sqrt{5},+∞})$ | C. | $({\frac{{\sqrt{5}}}{2},\sqrt{5}})$ | D. | $({1,\frac{{\sqrt{5}}}{2}})∪({\sqrt{5},+∞})$ |
 某校从参加高二年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3 (结果保留一位小数).
某校从参加高二年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3 (结果保留一位小数).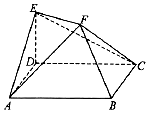 如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.
如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.