题目内容
14.“a>0,b>0”是“$ab<{({\frac{a+b}{2}})^2}$”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 结合基本不等式和充要条件的定义,分析“a>0,b>0”与“$ab<{({\frac{a+b}{2}})^2}$”的关系,可得答案.
解答 解:“a>0,b>0”时,$\frac{a+b}{2}≥\sqrt{ab}$,当a=b时,“$ab<{({\frac{a+b}{2}})^2}$”不成立,
故“a>0,b>0”是“$ab<{({\frac{a+b}{2}})^2}$”的不充分条件,
“$ab<{({\frac{a+b}{2}})^2}$”时,a,b可以异号,故“a>0,b>0”不一定成立,
故“a>0,b>0”是“$ab<{({\frac{a+b}{2}})^2}$”的既不充分也不必要条件,
故选:D
点评 本题考查的知识点是充要条件,正确理解充要条件的概念是解答的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
9.若命题p:?x0>0,|x0|≤1,则命题p的否定是( )
| A. | ?x>0,|x|>1 | B. | ?x>0,|x|≥1 | C. | ?x≤0,|x|<1 | D. | ?x≤0,|x|≤1 |
6.函数y=lg(|x|+1)的图象大致是( )
| A. | 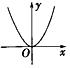 | B. | 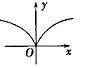 | C. | 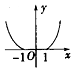 | D. | 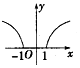 |
3.$sin\frac{11π}{3}$的值为( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |