题目内容
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F2的坐标是(4,0),过F2引圆x2+y2=a2的两条切线,切点分别为A,B,∠AOB=120°(O为坐标原点),则双曲线的标准方程为$\frac{{x}^{2}}{64}-\frac{{y}^{2}}{48}=1$.分析 根据题意可先求得∠AOF利用OF和OA,在直角三角形中求得双曲线的离心率.然后求解双曲线方程.
解答 解:如图,由题知OA⊥AF,OB⊥BF且∠AOB=120°,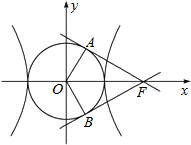
∴∠AOF=60°,又OA=a,
OF=c,
∴$\frac{a}{c}$=$\frac{OA}{OF}$=cos60°=$\frac{1}{2}$,
∴$\frac{c}{a}$=2.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F2的坐标是(4,0),可得c=4,则a=8,则b2=48,
所求双曲线方程为:$\frac{{x}^{2}}{64}-\frac{{y}^{2}}{48}=1$.
故答案为:$\frac{{x}^{2}}{64}-\frac{{y}^{2}}{48}=1$.
点评 本题主要考查了双曲线的简单性质.解题的过程中采用了数形结合的思想,使问题的解决更直观.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
2.已知圆(x+1)2+y2=2,则其圆心和半径分别为( )
| A. | (1,0),2 | B. | (-1,0),2 | C. | (1,0),$\sqrt{2}$ | D. | (-1,0),$\sqrt{2}$ |
20.已知角θ的顶点与原点重合,始边与x轴正半轴重合,终边过点P(-1,2),则tan2θ=( )
| A. | $\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{4}{3}$ |
7.已知$f(x)=sin(2017x+\frac{π}{6})+cos(2017x-\frac{π}{3})$的最大值为A,若存在实数x1,x2使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为72.
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为72.