题目内容
17.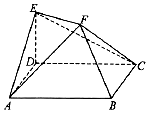 如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.
如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.(1)求证:平面EAC⊥垂直平面BDEF;
(2)求几何体ABCDEF的体积.
分析 (1)由ED⊥平面ABCD可得ED⊥AC,再由四边形ABCD是菱形,得BD⊥AC,然后利用线面垂直的判定可得AC⊥平面BDEF.从而得到平面EAC⊥平面BDEF;
(2)设AC∩BD=O,连结FO,由EF∥DO,且EF=DO,可得四边形EFOD是平行四边形,再由ED⊥平面ABCD,可得EO⊥DO,进一步得到AC⊥平面BDEF.
∴点A到平面BDEF的距离等于就是△ABD边BD上的高,求解直角三角形求得点A到平面BDEF的距离,再由几何体ABCDEF的体积V=VA-BDEF+VC-BDEF=2VA-BDEF求得答案.
解答 (1)证明:∵ED⊥平面ABCD,AC?平面ABCD,
∴ED⊥AC,
∵四边形ABCD是菱形,
∴BD⊥AC,
又ED∩DB=D,
∴AC⊥平面BDEF.
又AC?平面EAC,故平面EAC⊥平面BDEF;
(2)设AC∩BD=O,连结FO,∵EF∥DO,且EF=DO,
∴四边形EFOD是平行四边形,
又ED⊥平面ABCD,可得EO⊥DO,
∴四边形EFOD是矩形.
∵AC⊥平面BDEF.
∴点A到平面BDEF的距离等于就是△ABD边BD上的高,
且高$h=2sin{60°}=\sqrt{3}$.
∴几何体ABCDEF的体积V=VA-BDEF+VC-BDEF=2VA-BDEF=2×$\frac{1}{3}×\frac{1}{2}×(1+2)×\sqrt{3}=\sqrt{3}$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等体积法求多面体的体积,属中档题.

练习册系列答案
相关题目
7.已知$f(x)=sin(2017x+\frac{π}{6})+cos(2017x-\frac{π}{3})$的最大值为A,若存在实数x1,x2使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
8.在某项体育比赛中,五位裁判为一选手打出的分数如下:
92 89 95 91 93
去掉一个最高分和一个最低分后,所剩数的平均值和方差分别为( )
92 89 95 91 93
去掉一个最高分和一个最低分后,所剩数的平均值和方差分别为( )
| A. | 92,4 | B. | 93,5 | C. | 93,4 | D. | 92,$\frac{2}{3}$ |
9.若命题p:?x0>0,|x0|≤1,则命题p的否定是( )
| A. | ?x>0,|x|>1 | B. | ?x>0,|x|≥1 | C. | ?x≤0,|x|<1 | D. | ?x≤0,|x|≤1 |
6.函数y=lg(|x|+1)的图象大致是( )
| A. | 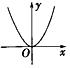 | B. | 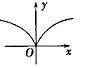 | C. | 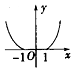 | D. |  |