题目内容
19.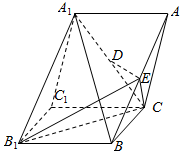 如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.
如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.(1)求证:ED∥平面BB1C1C;
(2)若AB=$\sqrt{2}$BB1,求证:A1B⊥平面B1CE.
分析 (1)连结AC1,BC1,则DE∥BC1,由此能证明ED∥平面BB1C1C.
(2)推导出CE⊥AB,从而CE⊥平面ABB1A1,进而CE⊥A1B,再推导出Rt△A1B1B∽Rt△B1BE,从而A1B⊥B1E,由此能证明A1B⊥平面B1CE.
解答 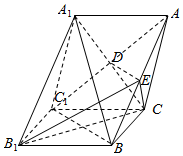 证明:(1)连结AC1,BC1
证明:(1)连结AC1,BC1
∵AA1C1C是矩形,D是A1C的中点,∴D是AC1的中点,
在△AA1C1C中,∵D、E分别是AC1、AB的中点,
∴DE∥BC1,
∵DE?平面BB1C1C,BC1?平面BB1C1C,
∴ED∥平面BB1C1C.
(2)∵△ABC是正三角形,E是AB的中点,∴CE⊥AB,
又∵正三棱柱A1B1C1-ABC中,平面ABC⊥平面ABB1A1,交线为AB,
∴CE⊥平面ABB1A1,
∴CE⊥A1B,
在矩形ABB1A1中,∵$\frac{{A}_{1}{B}_{1}}{{B}_{1}B}=\sqrt{2}=\frac{{B}_{1}B}{BE}$,
∴Rt△A1B1B∽Rt△B1BE,∴∠B1A1B=∠BB1E,
∴∠B1A1B+∠A1B1E=∠BB1E+∠A1B1E=90°,
∴A1B⊥B1E,
∵CE,B1E?平面B1CE,CE∩B1E=E,
∴A1B⊥平面B1CE.
点评 本题考查线面平行、线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
5.在△ABC中,若角A、B、C 的对边分别为a,b,c,且atanB=5,bsinA=4,则a等于( )
| A. | $\frac{15}{4}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{20}{3}$ |
4.已知两条不同的直线a,b,三个不同的平面α,β,γ,下列说法正确的是( )
| A. | 若a∥α,b⊥a,则b∥α | B. | 若a∥α,a∥β,则α∥β | C. | 若α⊥β,a⊥α,则a∥β | D. | 若α⊥γ,β∥γ,则α⊥β |
11.原点O(0,0)与点A(-4,2)关于直线l对称,则直线l的方程是( )
| A. | x+2y=0 | B. | 2x-y+5=0 | C. | 2x+y+3=0 | D. | x-2y+4=0 |
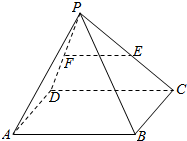 如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?
如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?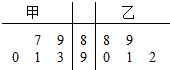 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.