��Ŀ����
14����ֱ������ϵxoy�У�����C1�IJ�������Ϊ$\left\{{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}}\right.$������Ϊ����������ԭ��OΪ���㣬x��������Ϊ���ᣬ����������ϵ������C2�ļ����귽��Ϊ��sin����+$\frac{��}{4}$��=4$\sqrt{2}$������������C1����ͨ����������C2��ֱ�����귽�̣�
������PΪ����C1�ϵĶ��㣬���P��C2�ϵ�ľ������Сֵ��
���� ��I������cos2��+sin2��=1�������õ�C1����ͨ���̣��������귽�����չ�����ɵõ�ֱ�����귽�̣�
��II������C1�IJ����������P��C2�ľ��룬�������Ǻ�������������������Сֵ��
��� �⣺��I����$\left\{{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}}\right.$��cos��=$\frac{x}{\sqrt{3}}$��sin��=y��������C1����ͨ������$\frac{{x}^{2}}{3}+{y}^{2}=1$��
��$��sin����+\frac{��}{4}��=4\sqrt{2}$�����sin��+��cos��=8����x+y-8=0��������C2��ֱ�����귽��ʱx+y-8=0��
��II����P�����꣨$\sqrt{3}cos��$��sin��������P��ֱ��C2�ľ���d=$\frac{|\sqrt{3}cos��+sin��-8|}{\sqrt{2}}$=$\frac{|2sin����+\frac{��}{3}��-8|}{\sqrt{2}}$��
�൱sin����+$\frac{��}{3}$��=1ʱ��dȡ����Сֵ$\frac{6}{\sqrt{2}}$=3$\sqrt{2}$��
���� ���⿼���˲������̣������귽����ֱ�����귽�̵Ļ��������������¾��빫ʽ����ֵ�����ڻ����⣮

��ϰ��ϵ�д�
 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�
�����Ŀ
6�����ɷ���x2-y2=0��x2+��y-b��2=2����ɵķ��������������鲻ͬ��ʵ���⣬��ʵ��b��ȡֵ��Χ�ǣ�������
| A�� | $b��2\sqrt{2}$��$b��-2\sqrt{2}$ | B�� | b��2��b��-2 | C�� | -2��b��2 | D�� | $-2\sqrt{2}��b��2\sqrt{2}$ |
3�����⣺����x2��1����x��-1��x��1������������ǣ�������
| A�� | ��x2��1����-1��x��1 | B�� | ��-1��x��1����x2��1 | ||
| C�� | ��-1��x��1����x2��1 | D�� | ��x��-1��x��1����x2��1 |
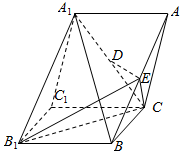 ��ͼ����������A1B1C1-ABC����D��E�ֱ���A1C��AB���е㣮
��ͼ����������A1B1C1-ABC����D��E�ֱ���A1C��AB���е㣮