题目内容
5.在△ABC中,若角A、B、C 的对边分别为a,b,c,且atanB=5,bsinA=4,则a等于( )| A. | $\frac{15}{4}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{20}{3}$ |
分析 首先由正弦定理求出asinB的值,然后利用弦切互化关系结合已知条件即可求出cosB,再由cosB求得sinB、tanB,则求得a.
解答 解:由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,又bsinA=4,∴asinB=bsinA=4,
又atanB=5,即$\frac{asinB}{cosB}=5$,
∴cosB=$\frac{4}{5}$;
则sinB=$\sqrt{1-co{s}^{2}B}=\sqrt{1-(\frac{4}{5})^{2}}=\frac{3}{5}$,
∴tanB=$\frac{3}{4}$,
∴a=$5×\frac{4}{3}=\frac{20}{3}$,
故选:D.
点评 本题主要考查正弦定理、弦切互化关系及余弦的倍角公式,属中档题.

练习册系列答案
相关题目
16.某小区的绿化建设有如下统计数据:
如果以后几年继续依次建设速度发展绿化,那么到哪一年该小区的绿化覆盖率可达到24%?
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 绿化覆盖率(%) | 18.0 | 18.6 | 19.2 | 19.8 | 20.4 |
20.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
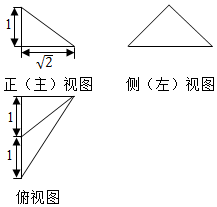

| A. | 2+2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 4+2$\sqrt{2}$ | D. | 4+$\sqrt{2}$ |
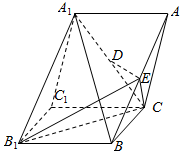 如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.
如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.