题目内容
4.已知两条不同的直线a,b,三个不同的平面α,β,γ,下列说法正确的是( )| A. | 若a∥α,b⊥a,则b∥α | B. | 若a∥α,a∥β,则α∥β | C. | 若α⊥β,a⊥α,则a∥β | D. | 若α⊥γ,β∥γ,则α⊥β |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:对于A,若a∥α,b⊥a,则b∥α,b与α相交或b?α,不正确;
对于B,若a∥α,a∥β,则α∥β或α,β相交,不正确;
对于C,若α⊥β,a⊥α,则a∥β或a?β,不正确;
对于D,若α⊥γ,β∥γ,在β内存在直线与α垂直,根据平面与平面垂直的判定,可得α⊥β,正确.
故选:D.
点评 本题考查面面垂直、平行的判定和线面平行的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.若命题p是假命题,命题q是真命题,则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ?p是假命题 | D. | ¬q是假命题 |
16.如图,在平行六面体ABCD-A′B′C′D′中,若$\overrightarrow{AB}=\vec a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{AA'}=\overrightarrow c$,则$\overrightarrow{BM}$=( )
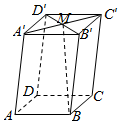

| A. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
14.若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则点(a,b)于圆心C之间的最小距离是( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
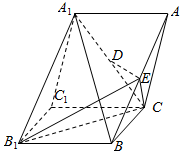 如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.
如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.