题目内容
9.已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则($\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$)•$\overrightarrow{c}$的最大值是$\sqrt{2}$-1.分析 |$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,不妨设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(cosθ,sinθ)(θ∈[0,2π)),代入化简利用三角函数的单调性最值即可得出.
解答 解:∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
不妨设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(cosθ,sinθ)(θ∈[0,2π))
则($\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$)•$\overrightarrow{c}$=(1-cosθ)•cosθ+(1-sinθ)•sinθ=sinθ+cosθ-1=$\sqrt{2}sin(θ+\frac{π}{4})$-1$≤\sqrt{2}$-1,
∴($\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$)•$\overrightarrow{c}$的最大值是$\sqrt{2}$-1.
故答案为:$\sqrt{2}$-1.
点评 本题考查了三角函数的单调性最值、向量的坐标运算数量积运算性质,考查了推理能力与计算能力,属于中档题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
| A. | 2+2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 4+2$\sqrt{2}$ | D. | 4+$\sqrt{2}$ |
| A. | x=0 | B. | $x=\frac{π}{4}$ | C. | $x=\frac{π}{2}$ | D. | x=π |
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
 已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )| A. | x1>x2,s12<s22 | B. | x1=x2,s12>s22 | C. | x1=x2,s12=s22 | D. | x1=x2,s12<s22 |
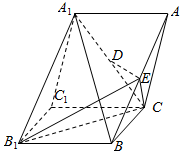 如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.
如图,正三棱柱A1B1C1-ABC,点D,E分别是A1C,AB的中点.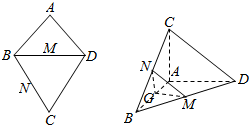 如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.
如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.